
科目:高中数学 来源: 题型:
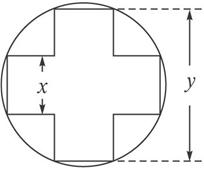
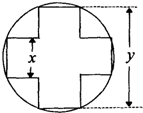 (2012•河北模拟)一变压器的铁芯截面为正十字型(两个全等的长方形,它们完全重合,把其中一个长方形绕中点旋转90°后而得的组合图叫正十字型),为保证所需的磁通量,要求十字应具有4
(2012•河北模拟)一变压器的铁芯截面为正十字型(两个全等的长方形,它们完全重合,把其中一个长方形绕中点旋转90°后而得的组合图叫正十字型),为保证所需的磁通量,要求十字应具有4| 5 |
查看答案和解析>>
科目:高中数学 来源:2014届陕西省高二上学期期中考试理科数学卷(解析版) 题型:解答题
一变压器的铁芯截面为正十字型,为保证所需的磁通量,要求十字应具有 的面积,问应如何设计十字型宽
的面积,问应如何设计十字型宽 及长
及长 ,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.
,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.
查看答案和解析>>
科目:高中数学 来源:期末题 题型:解答题
 cm2的面积,问应如何设计十字型宽x及y,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.
cm2的面积,问应如何设计十字型宽x及y,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.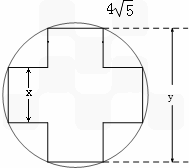
查看答案和解析>>
科目:高中数学 来源:《第3章 不等式》2013年单元测试卷3(解析版) 题型:解答题
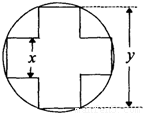 一变压器的铁芯截面为正十字型(两个全等的长方形,它们完全重合,把其中一个长方形绕中点旋转90°后而得的组合图叫正十字型),为保证所需的磁通量,要求十字应具有
一变压器的铁芯截面为正十字型(两个全等的长方形,它们完全重合,把其中一个长方形绕中点旋转90°后而得的组合图叫正十字型),为保证所需的磁通量,要求十字应具有 cm2的面积,问应如何设计十字型宽x及y,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.
cm2的面积,问应如何设计十字型宽x及y,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com