③④
分析:根据函数极值的定义,结合举反例得到①是错误的;根据积分的含义和有关公式,通过举出反例得到②是错误的;利用换元积分的方法,根据有关积分公式结合三角换元,计算得到③是正确的;根据积分的物理意义,质点的位移应该等于速度函数在某个时间段上的积分的值,利用积分公式可以通过计算,得到④是正确的.
解答:对于①,若f'(x
0)=0,则函数y=f(x)在x=x
0不一定取得极值,
比如函数f(x)=x
3,它的导数为f'(x)=3x
2,在x=0处满足f'(0)=0,
但函数f(x)是R上的增函数,在x=0处不能取得极值,故①错误;
对于②,若∫
abf(x)dx>0,则f(x)>0在[a,b]上不一定恒成立,
比如f(x)=x,∫
-12f(x)dx=
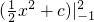
=
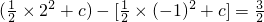
,其中c为常数,
满足∫
-12f(x)dx>0,但f(x)在[-1,2]上有正有负,故②错误;
对于③已知函数f(x)=
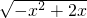
=
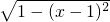
令x-1=cosα,则x=1+cosα,
其中

≤α≤π,x=0对应α=π,x=1对应α=

∴∫
01f(x)dx=
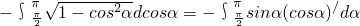
=
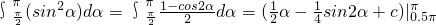
=
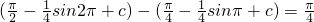
,其中c为常数,
所以∫
01f(x)dx的值为

,故③正确;
对于④,一质点在直线上以速度v=t
2-4t+3(m/s)运动,
从时刻t=0(s)到t=4(s)时质点运动的位移等于:
∫
04v(t)dt=
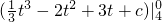
=
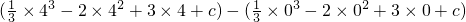
=

,其中c为常数,
从时刻t=0(s)到t=4(s)时质点运动的位移为

(m),故④正确.
故答案为:③④
点评:本题借助于命题真假的判断与应用,着重考查了函数的导数与极值之间的关系、积分的有关公式和积分的物理意义等知识点,属于中档题.

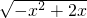 ,则∫01f(x)dx的值为
,则∫01f(x)dx的值为 ;
; (m)
(m)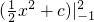 =
=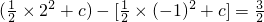 ,其中c为常数,
,其中c为常数,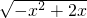 =
=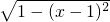
 ≤α≤π,x=0对应α=π,x=1对应α=
≤α≤π,x=0对应α=π,x=1对应α=
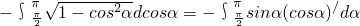
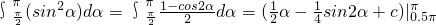
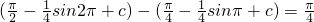 ,其中c为常数,
,其中c为常数, ,故③正确;
,故③正确;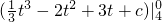
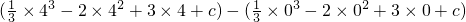 =
= ,其中c为常数,
,其中c为常数, (m),故④正确.
(m),故④正确. 

 应用题作业本系列答案
应用题作业本系列答案