Question

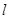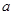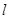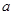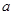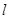已知直线₁：x＋y＋6＝0和₂：(－2)x＋3y＋2＝0，则₁∥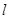₂的充要条件是＝________.

 

Answer 1

【答案】

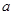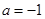
【解析】

试题分析：首先由两直线平行可得1×3=a×（a-2），解可得a=-1或3，分别验证可得a=-1时，则l₁∥l₂，即可得l₁∥l₂?a=-1；反之将a=-1代入直线的方程，可得l₁∥l₂，即有a=-1?l₁∥l₂；综合可得l₁∥l₂?a=-1，即可得答案．解：根据题意，若l₁∥l₂，则有1×3=a×（a-2），解可得a=-1或3，反之可得，当a=-1时，直线l₁：x-y+6=0，其斜率为1，直线l₂：-3x+3y-2=0，其斜率为1，且l₁与l₂不重合，则l₁∥l₂，当a=3时，，直线l₁：x+3y+6=0，直线l₂：x+3y+6=0，l₁与l₂重合，此时l₁与l₂不平行， l₁∥l₂?a=-1，反之，a=-1?l₁∥l₂，故l₁∥l₂?a=-1，故a=-1

考点：直线平行的判定方法

点评：本题考查直线平行的判定方法，利用解析几何的方法判断时，要注意验证两直线是否重合