
分析 (1)利用反证法进行证明;
(2)利用分析法证明即可.
解答 (1)证明:假设命题的结论不成立,即“2不能整除a”.(2分)
因为a是整数,故a是奇数,a可以表示为2m+1(m为整数),则a2=(2m+1)2=4m2+4m+1=2(2m2+2m)+1(6分)
即a2是奇数.
所以,2不能整除a2.这与已知“2能整除a2”相矛盾.
于是,“2不能整除a”这个假设错误,故2能整除a.(9分)
(2)证明:为证明$\frac{a+b}{2}≥\sqrt{ab}(a>0,b>0)$成立,
只需证$\frac{{{{(a+b)}^2}}}{4}≥ab$,即a2+b2+2ab≥4ab,(13分)
即a2+b2≥2ab,此式显然成立.(16分)
这样,就证明了$\frac{a+b}{2}≥\sqrt{ab}$.(18分)
点评 本题考查反证法、分析法,考查学生分析解决问题的能力,属于中档题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:填空题
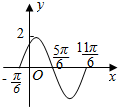 如图是$y=Asin(ωx+φ)(A>0,ω>0,0<φ<\frac{π}{2})$的图象,则其解析式为$y=2sin(x+\frac{π}{6})$.
如图是$y=Asin(ωx+φ)(A>0,ω>0,0<φ<\frac{π}{2})$的图象,则其解析式为$y=2sin(x+\frac{π}{6})$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com