
分析 ( I)当a=0时,设切点P(x0,ln(1+x0)),求出切线斜率,即可求切线的方程;
( II)求导数,分类讨论,利用导数的正负讨论函数f(x)在[0,+∞)的单调性;
( III)证明lnx-lny>x-y,同时0<x-y<1,有M(x-y)=-ln(x-y)+(x-y)-1>0,即x-y>ln(x-y)+1,即可证明:lnx-lny>ln(x-y)+1.
解答 ( I)解:当a=0时,f(x)=ln(1+x),设切点P(x0,ln(1+x0)),
∵$f'(x)=\frac{1}{1+x}$,∴$\frac{1}{{1+{x_0}}}=\frac{{ln({x_0}+1)}}{{{x_0}+1}}$,即x0=e-1,
∴切线的斜率$k=\frac{1}{e}$,切线的方程为x-ey+1=0;
( II)解:∵$f'(x)=\frac{1}{1+x}-a$,且当[0,+∞)时有$\frac{1}{1+x}∈({0,1}]$,
∴当a≤0时,$f'(x)=\frac{1}{1+x}-a≥0$在[0,+∞)上恒成立,即f(x)在[0,+∞)上单调递增
当a≥1时,$f'(x)=\frac{1}{1+x}-a≤0$在[0,+∞)上恒成立,即f(x)在[0,+∞)单调递减
当0<a<1时,f(x)在[0,$\frac{1-a}{a}$)上单调递増,在$(\frac{1-a}{a},+∞)$上单调递减;
( III)证明:当0<a<1时,f(x)的最大值为M(a)=-lna+a-1.
∵$M'(a)=\frac{a-1}{a}<0$在(0,1)上恒成立,
∴M(a)=-lna+a-1在(0,1)上单调递减,即M(a)=-lna+a-1>0,
∴-lny+y-1>-lnx+x-1,即lnx-lny>x-y,
同时0<x-y<1,有M(x-y)=-ln(x-y)+(x-y)-1>0,即x-y>ln(x-y)+1,
∴当0<y<x<1时,有lnx-lny>ln(x-y)+1.
点评 本题考查函数与导数,利用导数研究函数的单调性,极值,并利用单调性比较大小.考查了分类讨论、构造、推理计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{2}{3}$] | B. | (-∞,$\frac{1}{3}$] | C. | [$\frac{1}{3}$,+∞) | D. | [-$\frac{1}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 真,假,假 | B. | 真,真,假 | C. | 真,假,真 | D. | 假,假,真 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m>$\frac{5}{4}$ | B. | m<-$\frac{3}{4}$ | C. | m>1 | D. | m>-$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
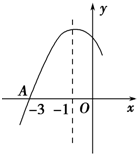 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出下面四个结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出下面四个结论:| A. | ②④ | B. | ①④ | C. | ②③ | D. | ①③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com