
【题目】如图所示,在直三棱柱ABC-A1B1C1中,CA=4,CB=4,CC1=2![]() ,∠ACB=90°,点M在线段A1B1上.
,∠ACB=90°,点M在线段A1B1上.

(1)若A1M=3MB1,求异面直线AM和A1C所成角的余弦值;
(2)若直线AM与平面ABC1所成角为30°,试确定点M的位置.
【答案】(1)![]() ;(2)线段A1B1的中点.
;(2)线段A1B1的中点.
【解析】
试题分析:本题考查用空间向量法解决立体几何问题,最简单的方法是建立空间直角坐标系,如以C为坐标原点,分别以CA,CB,CC1所在直线为x轴,y轴,z轴,建立如图所示的空间直角坐标系,写出各点坐标,(1)求得相应向量,异面直线AM和A1C所成角的余弦值就是cos〈![]() ,
,![]() 〉的绝对值;(2)先求得平面ABC1的法向量为n,因为点M在线段A1B1上,可设M(x,4-x,2
〉的绝对值;(2)先求得平面ABC1的法向量为n,因为点M在线段A1B1上,可设M(x,4-x,2![]() ),利用法向量n与向量
),利用法向量n与向量![]() 的夹角(锐角)与直线和平面所成的角互余可得,即由|cos〈n,
的夹角(锐角)与直线和平面所成的角互余可得,即由|cos〈n,![]() 〉|=
〉|=![]() 可求得
可求得![]() ,从而确定
,从而确定![]() 的位置.
的位置.
试题解析:方法一 (坐标法)
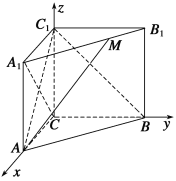
以C为坐标原点,分别以CA,CB,CC1所在直线为x轴,y轴,z轴,建立如图所示的空间直角坐标系,则C(0,0,0),A(4,0,0),A1(4,0,2![]() ),B1(0,4,2
),B1(0,4,2![]() ).
).
(1)因为A1M=3MB1,所以M(1,3,2![]() ).
).
所以![]() =(4,0,2
=(4,0,2![]() ),
),![]() =(-3,3,2
=(-3,3,2![]() ).
).
所以cos〈![]() ,
,![]() 〉=
〉=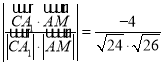 =-
=-![]() .
.
所以异面直线AM和A1C所成角的余弦值为![]() .
.
(2)由A(4,0,0),B(0,4,0),C1(0,0,2![]() ),
),
知![]() =(-4,4,0),
=(-4,4,0),![]() =(-4,0,2
=(-4,0,2![]() ).
).
设平面ABC1的法向量为n=(a,b,c),
由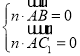 得
得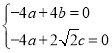
令a=1,则b=1,c=![]() ,
,
所以平面ABC1的一个法向量为n=(1,1,![]() ).
).
因为点M在线段A1B1上,所以可设M(x,4-x,2![]() ),
),
所以![]() =(x-4,4-x,2
=(x-4,4-x,2![]() ).
).
因为直线AM与平面ABC1所成角为30°,
所以|cos〈n,![]() 〉|=sin 30°=
〉|=sin 30°=![]() .
.
由|n![]()
![]() |=|n||
|=|n||![]() ||cos〈n,
||cos〈n,![]() 〉|,得
〉|,得
|1![]() (x-4)+1
(x-4)+1![]() (4-x)+
(4-x)+![]()
![]() 2
2![]() |
|
=2![]()
![]()
![]()
![]() ,
,
解得x=2或x=6.
因为点M在线段A1B1上,所以x=2,
即点M(2,2,2![]() )是线段A1B1的中点.
)是线段A1B1的中点.
方法二 (选基底法)
由题意得CC1⊥CA,CA⊥CB,CC1⊥CB,取![]() ,
,![]() ,
,![]() 作为一组基底,
作为一组基底,
则有|![]() |=|
|=|![]() |=4,|
|=4,|![]() |=2
|=2![]() ,
,
且![]()
![]()
![]() =
=![]()
![]()
![]() =
=![]()
![]()
![]() =0.
=0.
(1)由![]() =3
=3![]() ,则
,则![]() =
=![]()
![]() =
=![]()
![]() =
=![]()
![]() -
-![]()
![]() ,
,
∴![]() =
=![]() +
+![]() =
=![]() +
+![]()
![]() -
-![]()
![]() ,
,
且|![]() |=
|=![]()
![]() =-
=-![]() -
-![]() ,且|
,且|![]() |=2
|=2![]() ,
,
∴![]()
![]() =4
=4
∴cos〈![]() ,
,![]() 〉=
〉=![]() =
=![]() .
.
即异面直线AM与A1C所成角的余弦值为![]() .
.
(2)设A1M=λA1B1,则![]() =
=![]() +λ
+λ![]() -λ
-λ![]() .
.
又![]() =
=![]() -
-![]() ,
,![]() =
=![]() -
-![]() ,
,
设面ABC1的法向量为n=x![]() +y
+y![]() +z
+z![]() ,
,
则![]()
![]() =8z-16x=0,
=8z-16x=0,![]()
![]() =16y-16x=0,
=16y-16x=0,
不妨取x=y=1,z=2,
则n=![]() +
+![]() +2
+2![]() 且|n|=8,
且|n|=8,
|![]() |=
|=![]() ,
,![]() =16,
=16,
又AM与面ABC1所成的角为30°,则应有
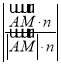 =
=![]() =
=![]() ,
,
得λ=![]() ,即M为A1B1的中点.
,即M为A1B1的中点.


科目:高中数学 来源: 题型:
【题目】经市场调查,某门市部的一种小商品在过去的20天内的日销售量(件)与价格(元)均为时间![]() (天)的函数,且日销售量近似满足函数
(天)的函数,且日销售量近似满足函数![]() (件),而且销售价格近似满足于
(件),而且销售价格近似满足于 (元).
(元).
(1)试写出该种商品的日销售额![]() 与时间
与时间![]() 的函数表达式;
的函数表达式;
(2)求该种商品的日销售额![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是圆
是圆![]() 内一个定点,
内一个定点,![]() 是圆上任意一点.线段
是圆上任意一点.线段![]() 的垂直平分线和半径
的垂直平分线和半径![]() 相交于点
相交于点![]() .
.
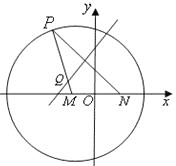
(Ⅰ)当点![]() 在圆上运动时,点
在圆上运动时,点![]() 的轨迹
的轨迹![]() 是什么曲线?并求出其轨迹方程;
是什么曲线?并求出其轨迹方程;
(Ⅱ)过点![]() 作直线
作直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 关于原点
关于原点![]() 的对称点为
的对称点为![]() ,求
,求![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P—ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.

(Ⅰ)证明PA//平面BDE;
(Ⅱ)求二面角B—DE—C的平面角的余弦值;
(Ⅲ)在棱PB上是否存在点F,使PB⊥平面DEF?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com