
为调查某社区居民的业余生活状况,研究这一社区居民在20:00-22:00时间段的休闲方式与性别的关系,随机调查了该社区80人,得到下面的数据表:

(I)根据以上数据,能否有99%的把握认为“在20:00-22:00时间段居民的休闲方式与性别有关系”?
(II)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量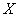 .求
.求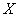 的数学期望和方差.
的数学期望和方差.
|
| 0.050 | 0.010 | 0.001 |
|
| 3.841 | 6.635 | 10.828 |
附: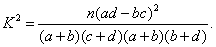
科目:高中数学 来源: 题型:
甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为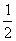 与
与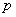 ,且乙投球2次均未命中的概率为
,且乙投球2次均未命中的概率为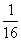 .
.
(Ⅰ)求乙投球的命中率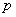 ; (Ⅱ)求甲投球2次,至少命中1次的概率;
; (Ⅱ)求甲投球2次,至少命中1次的概率;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com