
|
| x2 |
| 5-m |
| y2 |
| m+3 |
| x2 |
| 4 |
| y2 |
| 4 |
| x2 |
| 5-m |
| y2 |
| m+3 |
|
|
| x2 |
| 5-m |
| y2 |
| m+3 |


科目:高中数学 来源: 题型:
|
 |
| y |
查看答案和解析>>
科目:高中数学 来源:2011-2012年福建省四地六校高二第二次月考理科数学 题型:选择题
下列四个命题:
①使用抽签法,每个个体被抽中的机会相等;
②将十进制数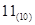 化为二进制数为
化为二进制数为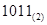 ;
;
③利用秦九韶算法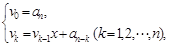
求多项式 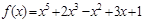 在
在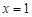 的值时
的值时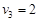 ;
;
④已知一个线性回归方程是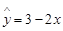 ,则变量
,则变量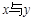 之间具有正相关关系.
之间具有正相关关系.
其中真命题的个数是 ( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2013届福建省高二上学期期末考试理科数学试卷 题型:选择题
下列四个命题:
① 使用抽签法,每个个体被抽中的机会相等;
② 将十进制数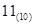 化为二进制数为
化为二进制数为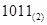 ;
;
③ 已知一个线性回归方程是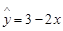 ,则变量
,则变量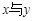 之间具有正相关关系;
之间具有正相关关系;
④ 将一组数据中的每个数都加上或减去同一个数后,方差恒不变.
其中真命题的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2012-2013学年新课标高二(上)第二次月考数学试卷(解析版) 题型:选择题
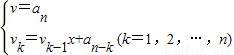 求多项式 f(x)=x5+2x3-x2+3x+1在x=1的值时v3=2;
求多项式 f(x)=x5+2x3-x2+3x+1在x=1的值时v3=2;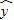 =3-2x,则变量x与y之间具有正相关关系.
=3-2x,则变量x与y之间具有正相关关系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com