
【题目】已知函数f(x)=lnx,g(x)=f(x)+ax2+bx,其中函数g(x)的图象在点(1,g(1))处的切线平行于x轴.
(1)确定a与b的关系;
(2)若a≥0,试讨论函数g(x)的单调性.
【答案】
(1)解:依题意得g(x)=lnx+ax2+bx,
则 ![]()
由函数g(x)的图象在点(1,g(1))处的切线平行于x轴得:g'(1)=1+2a+b=0,
∴b=﹣2a﹣1
(2)解:由(1)得 ![]() .
.
∵函数g(x)的定义域为(0,+∞),
∴当a=0时, ![]() .
.
由g'(x)>0,得0<x<1,由g'(x)<0,得x>1,
当a>0时,令g'(x)=0,得x=1或 ![]() ,
,
若 ![]() ,即
,即 ![]() ,
,
由g'(x)>0,得x>1或 ![]() ,
,
由g'(x)<0,得 ![]() ;
;
若 ![]() ,即
,即 ![]() ,
,
由g'(x)>0,得 ![]() 或0<x<1,
或0<x<1,
由g'(x)<0,得 ![]()
若 ![]() ,即
,即 ![]() ,在(0,+∞)上恒有g'(x)≥0
,在(0,+∞)上恒有g'(x)≥0
综上可得:当a=0时,函数g(x)在(0,1)上单调递增,在(1,+∞)上单调递减;
当 ![]() 时,函数g(x)在(0,1)上单调递增,
时,函数g(x)在(0,1)上单调递增,
在 ![]() 上单调递减,在
上单调递减,在 ![]() 上单调递增;
上单调递增;
当 ![]() 时,函数g(x)在(0,+∞)上单调递增;
时,函数g(x)在(0,+∞)上单调递增;
当 ![]() 时,函数g(x)在
时,函数g(x)在 ![]() 上单调递增,
上单调递增,
在 ![]() 上单调递减,在(1,+∞)上单调递增
上单调递减,在(1,+∞)上单调递增
【解析】(1)求出函数的导数,利用切线与x轴平行,推出结果.(2)求出函数的导数与函数g(x)的定义域,通过当a=0时,当a>0时,分别求解函数的极值点,判断函数的单调性,即可得到结论.


科目:高中数学 来源: 题型:
【题目】李老师骑自行车上班,最初以某一速度匀速行进,中途由于自行车发生故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,结果准时到校,在课堂上,李老师请学生画出自行车行进路程s(千米)与行进时间x(秒)的函数图象的示意图,你认为正确的是
A. 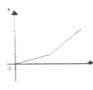 B.
B. 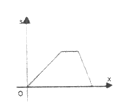
C. 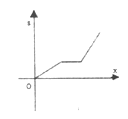 D.
D. 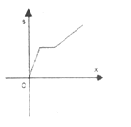
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图C,D是以AB为直径的圆上的两点,![]() ,F是AB上的一点,且
,F是AB上的一点,且![]() ,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知
,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知![]()

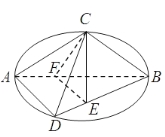
(1)求证:AD![]() 平面BCE
平面BCE
(2)求证:AD//平面CEF;
(3)求三棱锥A-CFD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() .
.
⑴若![]() 的定义域为
的定义域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
⑵当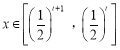 时,求函数
时,求函数![]() 的最小值
的最小值![]() ;
;
⑶是否存在非负实数![]() 、
、![]() ,使得函数
,使得函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,若存在,求出
,若存在,求出![]() 、
、![]() 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,函数f(x)=ax2+bx+c,若x0满足关于x的方程2ax+b=0,则下列选项的命题中为假命题的是( )
A.x∈R,f(x)≤f(x0)
B.x∈R,f(x)≥f(x0)
C.x∈R,f(x)≤f(x0)
D.x∈R,f(x)≥f(x0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}满足(1﹣a1008)5+2016(1﹣a1008)=1,(1﹣a1009)5+2016(1﹣a1009)=﹣1,数列{an}的前n项和记为Sn , 则( )
A.S2016=2016,a1008>a1009
B.S2016=﹣2016,a1008>a1009
C.S2016=2016,a1008<a1009
D.S2016=﹣2016,a1008<a1009
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与圆
与圆![]()
(1)若直线![]() 与圆
与圆![]() 相交于
相交于![]() 两个不同点,求
两个不同点,求![]() 的最小值;
的最小值;
(2)直线![]() 上是否存在点
上是否存在点![]() ,满足经过点
,满足经过点![]() 有无数对互相垂直的直线
有无数对互相垂直的直线![]() 和
和![]() ,它们分别与圆
,它们分别与圆![]() 和圆
和圆![]() 相交,并且直线
相交,并且直线![]() 被圆
被圆![]() 所截得的弦长等于直线
所截得的弦长等于直线![]() 被圆
被圆![]() 所截得的弦长?若存在,求出点
所截得的弦长?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com