练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    当k为何值时，直线y=kx+k-2与抛物线y2=4x有两个公共点,仅有一个公共点,无公共点？

    思路解析：可以考虑数形结合,也可以看方程组解的个数.

    解：由方程组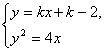消去y,得k2x2+2(k2-2k-2)+(k-2)2=0.

    （1）当k=0时，直线y=-2与抛物线y2=4x仅有一个公共点.

    （2）当k≠0时，Δ=4(k2-2k-2)2-4k2(k-2)2=-16(k2-2k-1).

    当k∈（1-，0）∪（0，1+）时，Δ＞0，直线与抛物线有两个公共点；

    当k=1±时，Δ=0，直线与抛物线仅有一个公共点；

    当k∈（-∞，1-）∪（1+，+∞）时，Δ＜0，直线与抛物线没有公共点.

    综合以上情况，当k∈（1-，0）∪（0，1+）时，直线与抛物线有两个公共点;当k=0或k=1±时，直线与抛物线仅有一个公共点;当k∈（-∞，1-）∪（1+，+∞）时，直线与抛物线没有公共点.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：044

    当k为何值时，直线y＝kx＋3过直线2x－y＋1＝0与y＝x＋5的交点?

    查看答案和解析>>

    科目：高中数学 来源：中学教材标准学案　数学　高二上册 题型：044

    当k为何值时，直线y＝kx＋2与椭圆＋y2＝1①有两个公共点；②有一个公共点；③没有公共点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：038

    　

    四边形OABC的四个顶点坐标分别为O(0，0)、A(6，2)、B(4，6)、C(2，6)，直线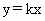(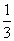＜k＜3)分四边形OABC为两部分，S表示靠近x轴一

    侧的那一部分的面积．

    (1)求S=f(k)的函数表达式；

    (2)当k为何值时，直线y=kx将四边形OABC分为面积相等的两部分．

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：044

    　

    四边形OABC的四个顶点坐标分别为O(0，0)、A(6，2)、B(4，6)、C(2，6)，直线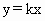(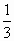＜k＜3)分四边形OABC为两部分，S表示靠近x轴一

    侧的那一部分的面积．

    (1)求S=f(k)的函数表达式；

    (2)当k为何值时，直线y=kx将四边形OABC分为面积相等的两部分．

    查看答案和解析>>

    同步练习册答案