
定义域为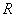 的函数
的函数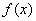 对任意的
对任意的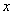 都有
都有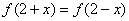 ,且其导函数
,且其导函数 满足:
满足: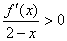 ,则当
,则当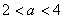 时,下列成立的是 ( )
时,下列成立的是 ( )
A.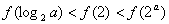 B.
B.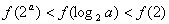
C.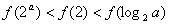 D.
D.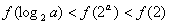
科目:高中数学 来源: 题型:
已知曲线C上任意一点到点F(1,0)的距离比到直线x+2=0的距离小1,点P(4,0).
(Ⅰ)求曲线C的方程;
(Ⅱ)设Q是曲线C上的动点,求|PQ|的最小值;
(Ⅲ)过点P的直线l与曲线C交于M、N两点,若△FMN的面积为6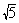 ,求直线l的方程。
,求直线l的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
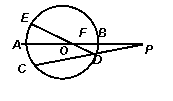
如图,⊙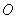 的直径
的直径 的延长线与弦
的延长线与弦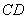 的延长线相交于点
的延长线相交于点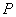 ,
,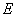 为⊙
为⊙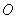 上一点,AE=AC ,
上一点,AE=AC ,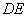 交
交 于点
于点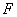 ,且
,且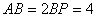 ,
,
(I)求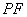 的长度.
的长度.
(II)若圆F与圆 内切,直线PT与圆F切于点T,求线段PT的长度
内切,直线PT与圆F切于点T,求线段PT的长度
 |
查看答案和解析>>
科目:高中数学 来源: 题型:
对于三次函数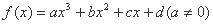 ,定义
,定义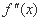 是
是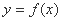 的导函数
的导函数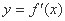 的导函数,若方程
的导函数,若方程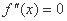 有实数解
有实数解 ,则称点
,则称点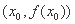 为函数
为函数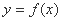 的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
①任意三次函数都关于点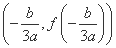 对称:
对称:
②存在三次函数 有实数解
有实数解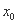 ,点
,点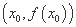 为函数
为函数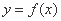 的对称中心;
的对称中心;
③存在三次函数有两个及两个以上的对称中心;
④若函数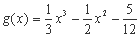 ,则
,则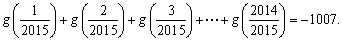
其中正确命题的序号为________ ____________(把所有正确命题的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
已知盒中装有大小一样,形状相同的3个白球与7个黑球,每次从中任取一个球并不放回,则在第1次取到的白球条件下,第2次取到的是黑球的概率为 ( )
A.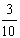 B.
B.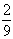 C.
C.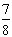 D.
D.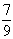
查看答案和解析>>
科目:高中数学 来源: 题型:
设f(x)= 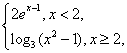
 则不等式f(x)>2的解集为 ( )
则不等式f(x)>2的解集为 ( )
(A)(1,2) (3,+∞) (B)(
(3,+∞) (B)(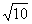 ,+∞)
,+∞)
(C)(1,2) (
(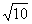 ,+∞) (D)(1,2)
,+∞) (D)(1,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com