
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求
时,求![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(Ⅲ)若对任意的![]() ,
,![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析;(Ⅲ)
;(Ⅱ)见解析;(Ⅲ)![]()
【解析】
(Ⅰ)利用函数和导函数的解析式求得切点和切线斜率,从而得到切线方程;(Ⅱ)通过导数可知单调性由![]() 的符号决定;分别在
的符号决定;分别在![]() 、
、![]() 两种情况下判断导函数的正负,从而得到原函数的单调区间;(Ⅲ)通过变量迁移可将问题变为
两种情况下判断导函数的正负,从而得到原函数的单调区间;(Ⅲ)通过变量迁移可将问题变为![]() 在
在![]() 上恒成立的问题;由
上恒成立的问题;由![]() 与
与![]() 的符号易判断
的符号易判断![]() ;构造函数
;构造函数![]() ,根据导函数正负可知
,根据导函数正负可知![]() 时满足题意;而当
时满足题意;而当![]() 时,由于存在
时,由于存在![]() 使得
使得![]() ,从而可知
,从而可知![]() 时,不等式不成立;由此总结可得结果.
时,不等式不成立;由此总结可得结果.
(Ⅰ)当![]() 时,
时,![]()
![]()
![]() ,
,![]()
![]() 函数
函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]()
(Ⅱ)由题意,![]()
![]()
(ⅰ)当![]() 时,
时,![]()
令![]() ,得
,得![]() ;
;![]() ,得
,得![]()
所以![]() 在
在![]() 单调递增,
单调递增,![]() 单调递减
单调递减
(ⅱ)当![]() 时,
时,![]()
令![]() ,得
,得![]() ;
;![]() ,得
,得![]() 或
或![]()
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() ,
,![]() 单调递减
单调递减
(Ⅲ)令![]() ,
,![]()
当![]() 时,
时,![]() ,
,![]() 单调递增,则
单调递增,则![]()
则![]() 对
对![]() 恒成立等价于
恒成立等价于![]()
即![]() ,对
,对![]() 恒成立.
恒成立.
(ⅰ)当![]() 时,
时,![]() ,
,![]() ,
,![]()
此时![]() ,不合题意,舍去
,不合题意,舍去
(ⅱ)当![]() 时,令
时,令![]() ,
,![]()
则![]()
其中对![]() ,
,![]()
令![]() ,则
,则![]() 在区间
在区间![]() 上单调递增
上单调递增
①当![]() 时,
时,![]()
所以对![]() ,
,![]() ,则
,则![]() 在
在![]() 上单调递增
上单调递增
故对任意![]() ,
,![]()
即不等式![]() 在
在![]() 上恒成立,满足题意
上恒成立,满足题意
②当![]() 时,由
时,由![]()
又![]() 且
且![]() 在区间
在区间![]() 上单调递增
上单调递增
所以存在唯一的![]() 使得
使得![]() ,且
,且![]() 时,
时,![]()
即![]() ,所以
,所以![]() 在区间
在区间![]() 上单调递减
上单调递减
则![]() 时,
时,![]() ,即
,即![]() ,不符合题意
,不符合题意
综上所述,![]()


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 是
是![]() 上的偶函数,对于任意
上的偶函数,对于任意![]() 都有
都有![]() 成立,当
成立,当![]() ,且
,且![]() 时,都有
时,都有![]() .给出以下三个命题:
.给出以下三个命题:
①直线![]() 是函数
是函数![]() 图像的一条对称轴;
图像的一条对称轴;
②函数![]() 在区间
在区间![]() 上为增函数;
上为增函数;
③函数![]() 在区间
在区间![]() 上有五个零点.
上有五个零点.
问:以上命题中正确的个数有( ).
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国中医学的发展,药用昆虫的使用相应愈来愈多.每年春暖以后至寒冬前,是昆虫大量活动与繁殖季节,易于采集各种药用昆虫.已知一只药用昆虫的产卵数![]() 与一定范围内的温度
与一定范围内的温度![]() 有关,于是科研人员在3月份的31天中随机挑选了5天进行研究,现收集了该种药用昆虫的5组观测数据如下表:
有关,于是科研人员在3月份的31天中随机挑选了5天进行研究,现收集了该种药用昆虫的5组观测数据如下表:
日期 | 2日 | 7日 | 15日 | 22日 | 30日 |
温度 | 10 | 11 | 13 | 12 | 8 |
产卵数 | 23 | 25 | 30 | 26 | 16 |
(1)从这5天中任选2天,记这两天药用昆虫的产卵分别为![]() ,
,![]() ,求事件“
,求事件“![]() ,
,![]() 均不小于25”的概率;
均不小于25”的概率;
(2)科研人员确定的研究方案是:先从这五组数据中任选2组,用剩下的3组数据建立![]() 关于
关于![]() 的线性回归方程,再对被选取的2组数据进行检验.
的线性回归方程,再对被选取的2组数据进行检验.
(ⅰ)若选取的是3月2日与30日的两组数据,请根据3月7日、15日和22日这三天的数据,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(ⅱ)若由线性回归方程得到的估计数据与选出的检验数据的误差均不超过2个,则认为得到的线性回归方程是可靠的,试问(ⅰ)中所得的线性回归方程是否可靠?
附:回归直线的斜率和截距的最小二乘估计公式分别为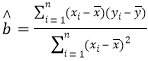 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次购物抽奖活动中,假设10张奖券中有一等奖奖券1张,可获价值50元的奖品,有二等奖奖券3张,每张可获价值10元的奖品,其余6张没有奖品.
(1)顾客甲从10张奖券中任意抽取1张,求中奖次数X的概率分布;
(2)顾客乙从10张奖券中任意抽取2张,
①求顾客乙中奖的概率;
②设顾客乙获得的奖品总价值Y元,求Y的概率分布及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数![]() ,
, ![]() +1.
+1.
(1)若![]() ,曲线y=f(x)与
,曲线y=f(x)与![]() 在x=0处有相同的切线,求b;
在x=0处有相同的切线,求b;
(2)若![]() ,求函数
,求函数![]() 的单调递增区间;
的单调递增区间;
(3)若![]() 对任意
对任意![]() 恒成立,求b的取值区间
恒成立,求b的取值区间
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品8件和B类产品15件,乙种设备每天能生产A类产品10件和B类产品25件,已知设备甲每天的租赁费300元,设备乙每天的租赁费400元,现车间至少要生产A类产品100件,B类产品200件,所需租赁费最少为__元![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com