
当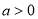 时,函数
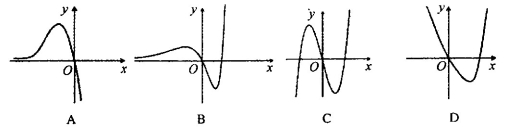
时,函数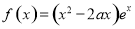 的图象大致是
的图象大致是
科目:高中数学 来源:2015届山东省菏泽市高二下学期期末考试理科数学试卷(解析版) 题型:解答题
(Ⅰ)已知复数z=1﹣i(i是虚数单位),若z2+a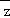 +b=3﹣3i,求实数a,b的值.
+b=3﹣3i,求实数a,b的值.
(Ⅱ)求二项式( +
+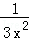 )10展开式中的常数项.
)10展开式中的常数项.
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
已知函数 .
.
(1)求函数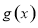 的单调区间;
的单调区间;
(2)若函数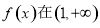 上是减函数,求实数a的最小值;
上是减函数,求实数a的最小值;
(3)若 ,使
,使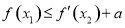 成立,求实数a的取值范围.
成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二下学期期中考试理科数学试卷(解析版) 题型:选择题
5名应届毕业生报考三所高校,每人报且仅报一所院校,则不同的报名方法的种数是( )
A. B.
B. C.
C. D.
D.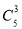
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
已知椭圆 的离心率为
的离心率为 ,
, 为椭圆在
为椭圆在 轴正半轴上的焦点,
轴正半轴上的焦点, 、
、 两点在椭圆
两点在椭圆 上,且
上,且 ,定点
,定点 .
.
(1)求证:当 时
时 ;
;
(2)若当 时有
时有 ,求椭圆
,求椭圆 的方程;
的方程;
(3)在(2)的椭圆中,当 、
、 两点在椭圆
两点在椭圆 上运动时,试判断
上运动时,试判断 是否有最大值,若存在,求出最大值,并求出这时
是否有最大值,若存在,求出最大值,并求出这时 、
、 两点所在直线方程,若不存在,给出理由.
两点所在直线方程,若不存在,给出理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com