
已知椭圆 的离心率为
的离心率为 ,
, 为椭圆在
为椭圆在 轴正半轴上的焦点,
轴正半轴上的焦点, 、
、 两点在椭圆
两点在椭圆 上,且
上,且 ,定点
,定点 .
.
(1)求证:当 时
时 ;
;
(2)若当 时有
时有 ,求椭圆
,求椭圆 的方程;
的方程;
(3)在(2)的椭圆中,当 、
、 两点在椭圆
两点在椭圆 上运动时,试判断
上运动时,试判断 是否有最大值,若存在,求出最大值,并求出这时
是否有最大值,若存在,求出最大值,并求出这时 、
、 两点所在直线方程,若不存在,给出理由.
两点所在直线方程,若不存在,给出理由.

(1)详见解析;(2)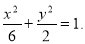 (3)存在,最大值为
(3)存在,最大值为 ,直线
,直线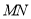 方程为
方程为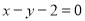 ,或
,或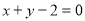
【解析】
试题分析:(1)设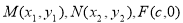 ,从而可得各向量的坐标。当
,从而可得各向量的坐标。当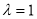 时
时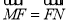 ,可得
,可得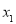 与
与 ,
,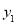 与
与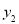 间的关系。将点
间的关系。将点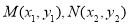 代入椭圆方程,结合
代入椭圆方程,结合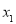 与
与 ,
,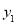 与
与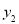 间的关系可得
间的关系可得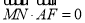 ,即
,即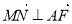 (2)当
(2)当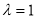 时由(1)知
时由(1)知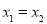 且
且 故可设
故可设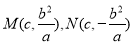 。根据
。根据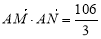 和
和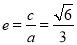 及
及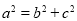 解方程组可求得
解方程组可求得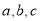 的值。(3)根据向量数量积公式及三角形面积公式分析可知
的值。(3)根据向量数量积公式及三角形面积公式分析可知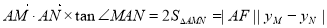 。设直线
。设直线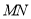 的方程为
的方程为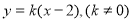 ,与椭圆方程联立消去
,与椭圆方程联立消去 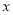 整理为关于
整理为关于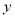 的一元二次方程,可得根与系数的关系。从而可用
的一元二次方程,可得根与系数的关系。从而可用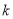 表示
表示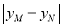 。用配方法求最值。注意讨论直线
。用配方法求最值。注意讨论直线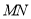 斜率不存在和斜率为0两种特殊情况。
斜率不存在和斜率为0两种特殊情况。
(1)设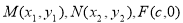 ,则
,则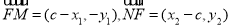 ,
,
当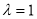 时,
时,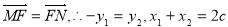 ,
,
由M,N两点在椭圆上,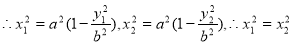
若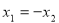 ,则
,则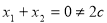 舍,
舍,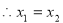

(2)当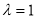 时,不妨设
时,不妨设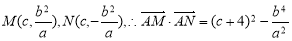
又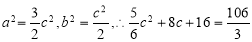 ,
,
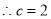 ,椭圆C的方程为
,椭圆C的方程为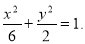
(3)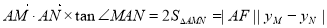 ,
,
设直线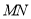 的方程为
的方程为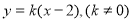
联立 ,得
,得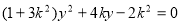 ,
,

记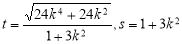 ,
,
则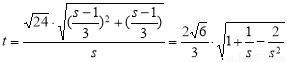
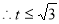 ,当
,当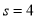 ,即
,即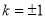 时取等号 .
时取等号 .
并且,当k=0时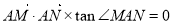 ,
,
当k不存在时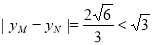
综上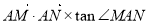 有最大值,最大值为
有最大值,最大值为
此时,直线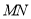 的方程为
的方程为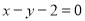 ,或
,或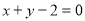
考点:1向量的数量积;2椭圆的简单几何性质及方程;3直线与椭圆的位置关系。


科目:高中数学 来源:2015届山东省菏泽市高二下学期期末考试文科数学试卷(解析版) 题型:选择题
下列推理中属于归纳推理且结论正确的是( )
A.由an=2n﹣1,求出S1=12,S2=22,S3=32,…,推断:数列{an}的前n项和Sn=n2
B.由f(x)=xcosx满足f(﹣x)=﹣f(x)对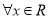 都成立,推断:f(x)=xcosx为奇函数
都成立,推断:f(x)=xcosx为奇函数
C.由圆x2+y2=r2的面积S=πr2,推断:椭圆 =1的面积S=πab
=1的面积S=πab
D.由 ,…,推断:对一切
,…,推断:对一切 ,(n+1)2>2n
,(n+1)2>2n
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
已知复数 (
( )
)
(1)若 是实数,求
是实数,求 的值;
的值;
(2)若 是纯虚数,求
是纯虚数,求 的值;
的值;
(3)若在复平面 内,
内, 所对应的点在第四象限,求
所对应的点在第四象限,求 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二下学期期中考试理科数学试卷(解析版) 题型:选择题
若函数 有极值点
有极值点 ,且
,且 ,若关于
,若关于 的方程
的方程 的不同实数根的个数是( )
的不同实数根的个数是( )
A.3 B.4 C.5 D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com