
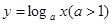 的图象上有
的图象上有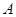 、
、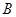 、
、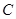 三点,横坐标分别为
三点,横坐标分别为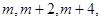 其中
其中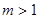 .
.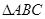 的面积
的面积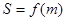 的表达式;
的表达式;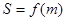 的值域.
的值域.科目:高中数学 来源:不详 题型:解答题
 ,有h(h(a))=a;
,有h(h(a))=a;
 ,使得h(m)=m,若m是函数h(x)的中介元,记
,使得h(m)=m,若m是函数h(x)的中介元,记 时h(x)的中介元为xn,且
时h(x)的中介元为xn,且 ,若对任意的
,若对任意的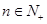 ,都有Sn<
,都有Sn<  ,求
,求 的取值范围;
的取值范围; =0,
=0, 时,函数y= h(x)的图像总在直线y=1-x的上方,求P的取值范围。
时,函数y= h(x)的图像总在直线y=1-x的上方,求P的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,深度为3m,如果池底每1
,深度为3m,如果池底每1 的造价为150元,池壁每1
的造价为150元,池壁每1 的造价为120元,怎样设计水池的底面长与宽的尺寸才能使总造价最低?最低总造价为多少元?(10分)
的造价为120元,怎样设计水池的底面长与宽的尺寸才能使总造价最低?最低总造价为多少元?(10分)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,上、下两边各空2
,上、下两边各空2 ,左、右两边各空1
,左、右两边各空1 .你如何设计海报的尺寸,才能使四周空白面积最小?
.你如何设计海报的尺寸,才能使四周空白面积最小?
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
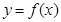 在
在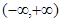 内有定义.对于给定的正数
内有定义.对于给定的正数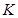 ,定义函数
,定义函数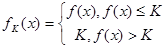 , 取函数
, 取函数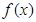 =
=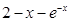 .若对任意的
.若对任意的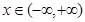 ,恒有
,恒有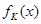 =
=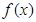 ,则 ( )
,则 ( ) A.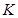 的最小值为1 的最小值为1 | B.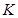 的最大值为2 的最大值为2 | C.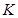 的最大值为1 的最大值为1 | D.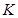 的最小值为2 的最小值为2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com