
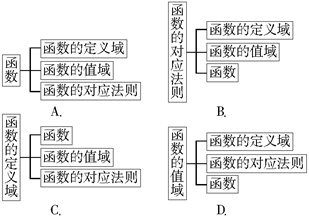
科目:高中数学 来源:不详 题型:解答题
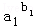
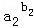 …
…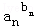 ≤1;
≤1; ≤
≤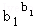
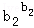 …
…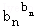 ≤b12+b22+…+bn2.
≤b12+b22+…+bn2.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ),B=[
),B=[ ,1],函数f(x)=
,1],函数f(x)=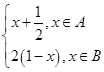 ,若x0∈A,且f[f(x0)]∈A,则x0的取值范围是( )
,若x0∈A,且f[f(x0)]∈A,则x0的取值范围是( )A.(0, ] ] | B.( , , ) ) |
C.( , , ] ] | D.[0, ] ] |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
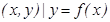 },若对于任意
},若对于任意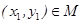 ,存在
,存在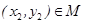 ,使得
,使得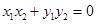 成立,则称集合M是“垂直对点集”.给出下列四个集合:
成立,则称集合M是“垂直对点集”.给出下列四个集合: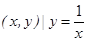 };
};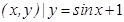 };
};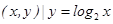 };
};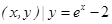 }.
}. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
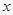 (单位:cm)满足关系:
(单位:cm)满足关系: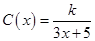 (
(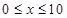 ,
,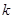 为常数),若不建隔热层,每年能源消耗费用为8万元.设
为常数),若不建隔热层,每年能源消耗费用为8万元.设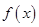 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.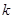 的值及
的值及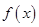 的表达式;
的表达式;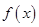 达到最小?并求出最小值.
达到最小?并求出最小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.-1<x<0 | B.-2<x<1 |
| C.-2<x<0 | D.0<x<1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com