
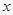 (单位:cm)满足关系:
(单位:cm)满足关系: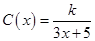 (
(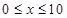 ,
,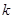 为常数),若不建隔热层,每年能源消耗费用为8万元.设
为常数),若不建隔热层,每年能源消耗费用为8万元.设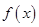 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.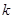 的值及
的值及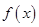 的表达式;
的表达式;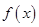 达到最小?并求出最小值.
达到最小?并求出最小值. ;(2)即隔热层修建
;(2)即隔热层修建 厚时,总费用
厚时,总费用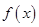 达到最小,最小值为70万元.
达到最小,最小值为70万元.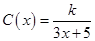 (0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.我们可得C(0)=8,得k=40,进而得到C(x)=
(0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.我们可得C(0)=8,得k=40,进而得到C(x)=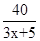 .建造费用为C1(x)=6x,则根据隔热层建造费用与20年的能源消耗费用之和为f(x),我们不难得到f(x)的表达式.
.建造费用为C1(x)=6x,则根据隔热层建造费用与20年的能源消耗费用之和为f(x),我们不难得到f(x)的表达式.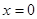 时,
时,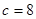 ,
, ,
,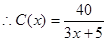 2分
2分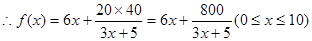 4分
4分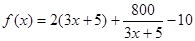 , 5分
, 5分 ,
, .
. 这时
这时 ,因此
,因此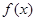 的最小值为70.
的最小值为70. 厚时,总费用
厚时,总费用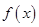 达到最小,最小值为70万元. 8分
达到最小,最小值为70万元. 8分

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源:不详 题型:解答题
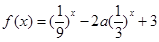
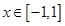
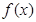 的最小值记为
的最小值记为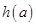 ,求
,求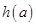 的解析式.
的解析式.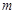 ,
,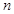 同时满足以下条件:①
同时满足以下条件:①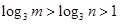 ;②当
;②当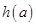 的定义域为[
的定义域为[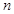 ,
,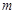 ]时,值域为[
]时,值域为[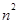 ,
,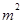 ];若存在,求出
];若存在,求出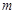 ,
,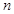 的值;若不存在,说明理由.
的值;若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
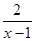 的定义域是(-∞,1)∪[2,5),则其值域是( )
的定义域是(-∞,1)∪[2,5),则其值域是( )A.(-∞,0)∪( ,2] ,2] | B.(-∞,2] |
C.(-∞, )∪[2,+∞) )∪[2,+∞) | D.(0,+∞) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
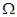 为平面直角坐标系
为平面直角坐标系 中的点集,从
中的点集,从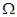 中的任意一点
中的任意一点 作
作 轴、
轴、 轴的垂线,垂足分别为
轴的垂线,垂足分别为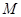 ,
, ,记点
,记点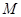 的横坐标的最大值与最小值之差为
的横坐标的最大值与最小值之差为 ,点
,点 的纵坐标的最大值与最小值之差为
的纵坐标的最大值与最小值之差为 .如果
.如果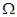 是边长为1的正方形,那么
是边长为1的正方形,那么 的取值范围是( )
的取值范围是( )A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
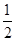 x2+bln(x+2)在(-1,+∞)上是减函数,则b的取值范围是( )
x2+bln(x+2)在(-1,+∞)上是减函数,则b的取值范围是( )| A.[-1,+∞) | B.(-1,+∞) |
| C.(-∞,-1] | D.(-∞,-1) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 的单位:s,v的单位:m/s)行驶至停止,在此期间汽车继续行驶的距离(单位:m)是( )
的单位:s,v的单位:m/s)行驶至停止,在此期间汽车继续行驶的距离(单位:m)是( )| A.1+25ln5 | B.8+25ln | C.4+25ln5 | D.4+50ln2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com