Question

13．设点P（x，y）为圆x²+y²=1上任-点．求下列两个式子的取值范围．
（1）$\frac{y-2}{x+1}$；
（2）x²+y²-2x+6y+1．

Answer 1

分析 （1）设$\frac{y-2}{x+1}=k$，得到kx-y+k+2=0，然后，利用圆心到直线的距离，确定其取值范围；
（2）设z=x²+y²-2x+6y+1=（x-1）²+（y+3）²-9．则z的几何意义圆上的点到定点A（1，-3）距离的平方减9，根据距离公式即可求出z的取值范围．

解答 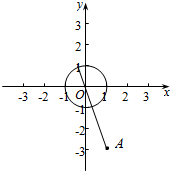解：（1）设$\frac{y-2}{x+1}=k$，即kx-y+k+2=0，
圆心到直线的距离为d=$\frac{|k+2|}{\sqrt{1+{k}^{2}}}$≤1，
∴k≤-$\frac{3}{4}$，
∴$\frac{y-2}{x+1}$的取值范围：（$-∞，-\frac{3}{4}$]．
（2）令=x²+y²-2x+6y+1=（x-1）²+（y+3）²-9．
可得（x-1）²+（y+3）²=z+9，
表达式（x-1）²+（y+3）²的最值就是圆的圆心与定点A（1，-3）的距离的平方，
|PA|_min=$\sqrt{（0-1）^{2}+（0+3）^{2}}$-1=$\sqrt{10}$-1，
z的最小值为：${（\sqrt{10}-1）}^{2}-9$=2-2$\sqrt{10}$，
z的最大值为：${（\sqrt{10}+1）}^{2}-9$=2+2$\sqrt{10}$，
x²+y²-2x+6y+1的取值范围：[2-2$\sqrt{10}$，2+2$\sqrt{10}$]．

点评 本题主要考查直线与圆的位置关系的判断，圆的方程的综合应用，根据函数的几何意义是解决本题的关键．