
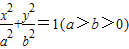 上任一点P到两焦点的距离的和为6,离心率为
上任一点P到两焦点的距离的和为6,离心率为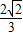 ,A、B分别是椭圆的左右顶点.
,A、B分别是椭圆的左右顶点.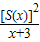 ,求函数f(x)的最大值.
,求函数f(x)的最大值.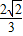 ,求出几何量,从而可求椭圆的标准方程;
,求出几何量,从而可求椭圆的标准方程;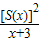 ,利用导数知识,可求函数f(x)的最大值.
,利用导数知识,可求函数f(x)的最大值.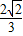 ,
,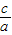 =
=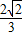 ,
,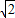
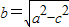 =1
=1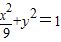 ;
;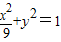 上得
上得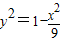 ,且S(x)=
,且S(x)=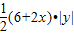
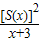 =(x+3)(
=(x+3)(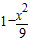 )=
)=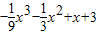 (0<x<3)
(0<x<3) (x-1)(x+3)
(x-1)(x+3)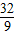 .
.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
| [S(x)]2 |
| x+3 |
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 人教课标高二版(A选修1-1) 2009-2010学年 第26期 总第182期 人教课标版(A选修1-1) 题型:022
下列有关圆锥曲线的命题,其中正确的是________.
①双曲线![]() -
-![]() =1的离心率为
=1的离心率为![]() ;
;
②抛物线y2=-6x的焦点坐标是(-3,0);
③椭圆x2+9y2=9上任一点P到两焦点的距离之和为6.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
| [S(x)]2 |
| x+3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com