Question

已知数列{a_n}是首项为1，公差为2的等差数列，对每一个k∈N^*，在a_k与a_k+1之间插入2^k-1个2，得到新数列{b_n}．设S_n，T_n 分别是数列{b_n}和数列{a_n}的前n项和．
（1）求数列{b_n}的前6项和S₆；
（2）a₁₀是数列{b_n}的第几项；
（3）若a_m是数列{b_n}的第f（m）项，试比较S_f（m）与2T_m的大小，并说明理由．

Answer 1

【答案】分析：（1）数列{b_n}中前6项依次为1，2，3，2，2，5，所以可求数列{b_n}的前6项和；
（2）因为在数列{bn}中，对每一个k∈N^*，在a_k与a_k+1之间插入2^k-1个2，所以a₁₀在数列{b_n}中的项数为：10+1+2+4+…+2⁸ 故问题得解；
（3）S_f（m）=2^m+m²-2又T_m=1+3+5+…+（2m-1）=m²，要比较S_f（m）与2T_m的大小，作差，再进行讨论即可．
解答：解：（1）∵数列{b_n}中前6项依次为1，2，3，2，2，5，∴数列{b_n}的前6项和S₆为1+2+3+2+2+5=15
（2）∵数列{b_n}中，对每一个k∈N^*，在a_k与a_k+1之间插入2^k-1个2，
∴a₁₀在数列{b_n}中的项数为10+1+2+4+…+2⁸=521
即a₁₀是数列{b_n}的第521项；
（3）a_n=2n-1，在数列{b_n}中，a_n及其前面所有项的和为1+3+…+（2m-1）+2+4+…+2^m-1=2^m+m²-2
即S_f（m）=2^m+m²-2又T_m=1+3+5+…+（2m-1）=m²
∴S_f（m）-2T_m=（2^m+m²-2）-2m²=2^m-（m²+2）…（10分）
当m=1时，2^m=2，m²+2=3，故2^m＜m²+2；
当m=2时，2^m=4，m²+2=6，故2^m＜m²+2；
当m=3时，2^m=8，m²+2=11，故2^m＜m²+2；
当m=4时，2^m=16，m²+2=18，故2^m＜m²+2； …（12分）
当
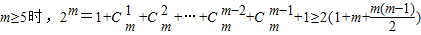
因而当m=1，2，3，4时，S_f（m）＜2T_m；
当m≥5时且m∈N^*时，S_f（m）＞2T_m…（14分）
点评：本题以等差数列为载体，考查新数列的理解．解决第（3）问的关键在于求出a_n及其前面所有项之和的表达式，再进行分类讨论，有一定的难度．