解:(1)令f(x
1)=f(x
2)
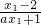
=
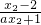
化简得:(2a+1)(x
1-x
2)=0
因为a>1.所以等式成立的唯一条件是:x
1=x
2.
∴函数的图象上不存在不同的两点,它们的函数值相同
(2)F(x)=a
x+f(x)=a
x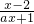
a>1,所以a
x在区间(-∞,0]上为增函数,而f(x)在区间(-∞,0]上也是增函数.
根据函数单调性的性质:在同一单调区间内增函数+增函数,还是增函数.
可得函数F(x)=a
x+f(x)在区间(-∞,0]上为增函数
又因为F(0)=-1
所以当x<0时,f(x)<-1
所以就不存在x<0,使得f(x)=0.
即方程F(x)=0没有负根
(3)a
x>0,
如果b<0,则:g(x)=(1-b)a
x-b,为单调递增函数,无最小值.
如果b≥0,则:
当a
x>b时,g(x)=(1-b)a
x-b,
当a
x<b时,g(x)=-(1+b)a
x+b,
因为在两个开区间内,g(x)都是单调函数.
所以,要取得最小值的条件是,在(-∞,b]为减函数,在[b,∞)为增函数.
所以:
1-b>0
-(1+b)<0
又∵b≥0
解得:0≤b<1
分析:(1)根据已知中函数f(x)=
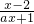
,我们令f(x
1)=f(x
2),然后代入函数的解析式,再根据实数的性质得到(2a+1)(x
1-x
2)=0,结合a>1,可得等式成立的唯一条件是:x
1=x
2.进而得到结论;
(2)由已知中函数F(x)=a
x+f(x),我们可以求出函数F(x)的解析式,进而根据基本初等函数的性质及函数单调性的性质判断出函数F(x)在区间(-∞,0]上的单调性,进而根据F(0)的值,得到结论;
(3)由已知中G(x)=|a
x-b|-b•a
x,我们分b<0和b≥0两种情况,进行分类讨论,分别讨论两种情况下函数的单调性,进而得到G(x)有最小值时,b的取值范围.
点评:本题考查的知识点是根的存在性及根的个数判断,函数最小值及其几何意义,其中(1)的关键是构造方程,然后根据已知条件得到等式成立的唯一条件是:x
1=x
2.(2)的关键是根据基本初等函数的性质及函数单调性的性质判断出函数F(x)在区间(-∞,0]上的单调性,(3)的关键确定分类标准,然后讨论各种情况下,函数的单调性并进而确定是否存在最小值.

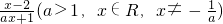 ;
;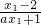 =
=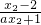
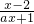
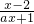 ,我们令f(x1)=f(x2),然后代入函数的解析式,再根据实数的性质得到(2a+1)(x1-x2)=0,结合a>1,可得等式成立的唯一条件是:x1=x2.进而得到结论;
,我们令f(x1)=f(x2),然后代入函数的解析式,再根据实数的性质得到(2a+1)(x1-x2)=0,结合a>1,可得等式成立的唯一条件是:x1=x2.进而得到结论;

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案