
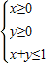 ,则
,则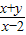 的取值范围是( )
的取值范围是( ) =1+
=1+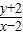 表示直线PQ的斜率再加1,将点Q移动并观察倾斜角的变化,可得
表示直线PQ的斜率再加1,将点Q移动并观察倾斜角的变化,可得 的最大值和最小值,从而得到
的最大值和最小值,从而得到 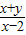 的取值范围.
的取值范围. 表示的平面区域,得如图的△ABO.
表示的平面区域,得如图的△ABO.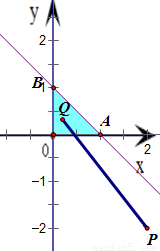
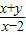 =1+
=1+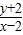 ,可得P(2,-2),点Q(x,y)是区域内的动点
,可得P(2,-2),点Q(x,y)是区域内的动点 =1+
=1+ ,表示直线PQ的斜率再加上1,
,表示直线PQ的斜率再加上1,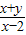 =1+
=1+ 的最大值为0,最小值为-1
的最大值为0,最小值为-1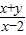 取值范围为[-1,0]
取值范围为[-1,0]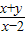 的取值范围,着重考查了二元一次不等式组表示的平面区域和简单的线性规划等知识,属于中档题.
的取值范围,着重考查了二元一次不等式组表示的平面区域和简单的线性规划等知识,属于中档题. 

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源:2011年广东省江门市普通高中高三调研数学试卷(理科)(解析版) 题型:选择题
 ,则
,则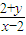 的取值范围是( )
的取值范围是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com