
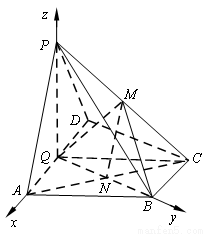
(本小题满分14分)如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=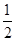 AD=1,CD=
AD=1,CD=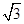 .
.
(1)求证:平面PQB⊥平面PAD;
(2)若二面角M-BQ-C为30°,设PM=tMC,
试确定t的值
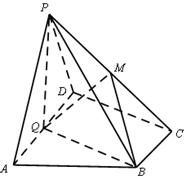
(1)∵AD // BC,BC=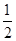 AD,Q为AD的中点,
AD,Q为AD的中点,
∴四边形BCDQ为平行四边形,∴CD // BQ . ∵∠ADC=90° ∴∠AQB=90°
即QB⊥AD.
又∵平面PAD⊥平面ABCD 且平面PAD∩平面ABCD=AD,
∴BQ⊥平面PAD. ∵BQ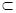 平面PQB,
平面PQB,
∴平面PQB⊥平面PAD. ……………………7分
另证:AD // BC,BC=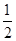 AD,Q为AD的中点,
∴ 四边形BCDQ为平行四边形,
AD,Q为AD的中点,
∴ 四边形BCDQ为平行四边形,
∴CD // BQ .∵ ∠ADC=90° ∴∠AQB=90°. ∵ PA=PD, ∴PQ⊥AD.
∵ PQ∩BQ=Q, ∴AD⊥平面PBQ. ∵ AD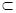 平面PAD,
平面PAD,
∴平面PQB⊥平面PAD.……7分
(2)∵PA=PD,Q为AD的中点, ∴PQ⊥AD.
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴PQ⊥平面ABCD.
如图,以Q为原点建立空间直角坐标系.
则平面BQC的法向量为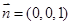 ;
;
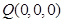 ,
,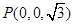 ,
,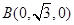 ,
,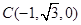 .
.
设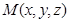 ,则
,则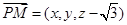 ,
,
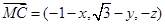 ,∵
,∵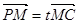 ,
,
∴ 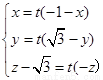 ,∴
,∴ 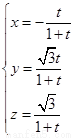 ……………………12分
……………………12分
在平面MBQ中,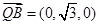 ,
,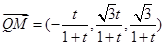 ,
,
∴ 平面MBQ法向量为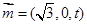 .
.
∵二面角M-BQ-C为30°,
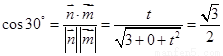 ,
,
∴ 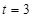 .
……………………14分
.
……………………14分
注:此小题若用几何法做也相应给分。
【解析】略


科目:高中数学 来源: 题型:
| 3 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)设椭圆C1的方程为![]() (a>b>0),曲线C2的方程为y=
(a>b>0),曲线C2的方程为y=![]() ,且曲线C1与C2在第一象限内只有一个公共点P。(1)试用a表示点P的坐标;(2)设A、B是椭圆C1的两个焦点,当a变化时,求△ABP的面积函数S(a)的值域;(3)记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个。设g(a)是以椭圆C1的半焦距为边长的正方形的面积,试求函数f(a)=min{g(a), S(a)}的表达式。
,且曲线C1与C2在第一象限内只有一个公共点P。(1)试用a表示点P的坐标;(2)设A、B是椭圆C1的两个焦点,当a变化时,求△ABP的面积函数S(a)的值域;(3)记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个。设g(a)是以椭圆C1的半焦距为边长的正方形的面积,试求函数f(a)=min{g(a), S(a)}的表达式。
查看答案和解析>>
科目:高中数学 来源:2011年江西省抚州市教研室高二上学期期末数学理卷(A) 题型:解答题
(本小题满分14分)
已知 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
.
(1)证明:数列 }是等比数列;
}是等比数列;
(2)设 ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式;
(3)记 ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
.
查看答案和解析>>
科目:高中数学 来源:2015届山东省威海市高一上学期期末考试数学试卷(解析版) 题型:解答题
(本小题满分14分)
某网店对一应季商品过去20天的销售价格及销售量进行了监测统计发现,第 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 天的销售量为
天的销售量为 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元.
(Ⅰ)写出销售额 关于第
关于第 天的函数关系式;
天的函数关系式;
(Ⅱ)求该商品第7天的利润;
(Ⅲ)该商品第几天的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省高三下学期第一次月考文科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行.
⑴ 求 ,
, 满足的关系式;
满足的关系式;
⑵ 若 上恒成立,求
上恒成立,求 的取值范围;
的取值范围;
⑶ 证明: (
( )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com