练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    给n个自上而下相连的正方形着黑色或白色，当n≤4时，在所有不同的着色方案中，黑色正方形互不相邻的着色方案如下图所示：
    由此推断，当n=6时，黑色正方形互不相邻的着色方案共有（    ）种，至少有两个黑色正方形相邻的着色方案共有（    ）种．（结果用数值表示）
    21；43
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

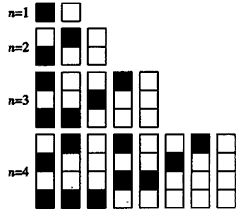
    15、给n个自上而下相连的正方形着黑色或白色．当n≤4时，在所有不同的着色方案中，黑色正方形互不相连的着色方案如图所示：
    由此推断，当n=6时，黑色正方形互不相邻的着色方案共有
    21
    种，至少有两个黑色正方形相邻的着色方案共有
    43
    种，（结果用数值表示）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

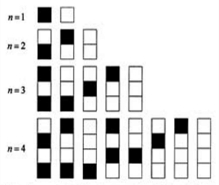
    给n个自上而下相连的正方形着黑色或白色．当n≤4时，在所有不同的着色方案中，黑色正方形互不相连的着色方案如图所示：由此推断，当n=6时，黑色正方形互不相连的着色方案共有多少种，至少有两个黑色正方形相连的着色方案共有多少种？

    查看答案和解析>>

    科目：高中数学 来源：2013届浙江省高二第一次月考理科数学试卷（解析版） 题型：填空题

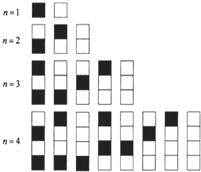
    给n个自上而下相连的正方形着黑色或白色，当n≤4时，在所有不同的着色方案中，黑色正方形互不相邻的着色方案如图1所示，由此推断，当n=6时，黑色正方形互不相邻的着色方案共有__________种，至少有两个黑色正方形相邻的着色方案共有_________.

    (结果用数值表示)

    n=1     

    n=2     

    n=3   

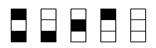
    n=4

     

    查看答案和解析>>

    科目：高中数学 来源：新课标高三数学组合、排列与组合的综合问题专项训练（河北） 题型：填空题

    给n个自上而下相连的正方形着黑色或白色，当n≤4时，在所有不同的着色方案中，黑色正方形互不相邻的着色方案如图1所示，由此推断，当n=6时，黑色正方形互不相邻的着色方案共有__________种，至少有两个黑色正方形相邻的着色方案共有_________.

    (结果用数值表示)

    n=1     

    n=2     

    n=3   

    n=4

     

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年福建师大附中高二（下）期末数学试卷（理科）（解析版） 题型：填空题

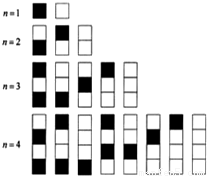    给n个自上而下相连的正方形着黑色或白色．当n≤4时，在所有不同的着色方案中，黑色正方形互不相连的着色方案如图所示：由此推断，当n=6时，黑色正方形互不相邻的着色方案共有    种，至少有两个黑色正方形相邻的着色方案共有    种，（结果用数值表示）

    查看答案和解析>>

    同步练习册答案