分析:(I)要证明线与线垂直,根据所给的直三棱柱的侧棱与底面垂直和根据三条边长得到的勾股定理,得到线面垂直,进而得到线线垂直.
(II)要证明线面平行,根据线面平行的判定定理,首先证明线与线平行,要写清楚两条线段的位置,得到结论.
(III)以C为原点建立空间直角坐标系C-xyz,写出要用的点的坐标,构造向量,根据线段的比值,得到向量的坐标,设出法向量,求出法向量,根据向量所成的角做出二面角.
解答: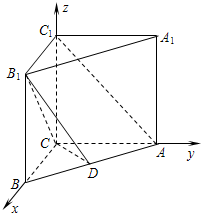
证明:(Ⅰ)在△ABC中,因为AB=5,AC=4,BC=3,
所以AC
2+BC
2=AB
2,所以AC⊥BC.
因为直三棱柱ABC-A
1B
1C
1,所以CC
1⊥AC.
因为BC∩AC=C,
所以AC⊥平面BB
1C
1C.
所以AC⊥B
1C.
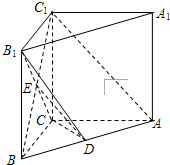
(Ⅱ)证明:连接BC
1,交B
1C于E,DE.
因为直三棱柱ABC-A
1B
1C
1,D是AB中点,
所以侧面BB
1C
1C为矩形,DE为△ABC
1的中位线,
所以DE∥AC
1.
因为DE?平面B
1CD,AC
1?平面B
1CD,
所以AC
1∥平面B
1CD.
(Ⅲ)解:由(Ⅰ)知AC⊥BC,
所以如图,以C为原点建立空间直角坐标系C-xyz.
则B(3,0,0),A(0,4,0),A
1(0,0,c),B
1(3,0,4).
设D(a,b,0)(a>0,b>0),
因为点D在线段AB上,且
=,即
=.
所以a=2,
b=,
=(-1,,0).
所以
=(3,0,4),
=(-3,4,0),
=(2,,0).
平面BCD的法向量为
=(0,0,1).
设平面B
1CD的法向量为
=(x,y,1),
由
•=0,
•=0,得
,
所以
x=-,y=2,
=(-,2,1).
设二面角B-CD-B
1的大小为θ,
所以
cosθ==.
所以二面角B-CD-B
1的余弦值为
.
点评:本题考查空间中直线与平面之间的平行和垂直关系,用空间向量求解两个平面的夹角,本题解题的关键是建立坐标系,把理论的推导转化成数字的运算.

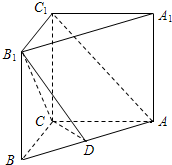 直三棱柱ABC-A1B1C1中,AB=5,AC=4,BC=3,AA1=4,点D在AB上.
直三棱柱ABC-A1B1C1中,AB=5,AC=4,BC=3,AA1=4,点D在AB上.
 证明:(Ⅰ)在△ABC中,因为AB=5,AC=4,BC=3,
证明:(Ⅰ)在△ABC中,因为AB=5,AC=4,BC=3,

 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=BB1=a,直线B1C与平面ABC成30°角.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=BB1=a,直线B1C与平面ABC成30°角. 如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是
如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是







