
【题目】设函数f(x)=丨x+a+1丨+丨x-![]() 丨,(a>0)。
丨,(a>0)。
(1)证明:f(x)≥5;
(2)若f(1)<6成立,求实数a的取值范围。
 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:
【题目】工人在安装一个正六边形零件时,需要固定如图所示的六个位置的螺丝,第一阶段,首先随意拧一个螺丝,接着拧它对角线上(距离它最远的,下同)螺丝,再随意拧第三个螺丝,第四个也拧它对角线上螺丝,第五个和第六个以此类推,但每个螺丝都不要拧死;第二阶段,将每个螺丝拧死,但不能连续拧相邻的2个螺丝。则不同的固定方式有 . 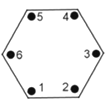
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨,生产每吨乙产品要用A原料1吨,B原料3吨。销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元,该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨,那么该企业可获得最大利润是___________万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司制定了一个激励销售人员的奖励方案:当销售利润不超过15万元时,按销售利润的10%进行奖励;当销售利润超过15万元时,若超过部分为A万元,则超出部分按2log5(A+1)进行奖励,没超出部分仍按销售利润的10%进行奖励.记奖金总额为y(单位:万元),销售利润为x(单位:万元).
(1)写出该公司激励销售人员的奖励方案的函数表达式;
(2)如果业务员老张获得5.5万元的奖金,那么他的销售利润是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=(x2﹣3)ex , 当m在R上变化时,设关于x的方程f2(x)﹣mf(x)﹣ ![]() =0的不同实数解的个数为n,则n的所有可能的值为( )
=0的不同实数解的个数为n,则n的所有可能的值为( )
A.3
B.1或3
C.3或5
D.1或3或5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 关于原点对称,
关于原点对称,![]() 恰为抛物线
恰为抛物线![]() :
:![]()
![]() 的焦点,点
的焦点,点![]() 在抛物线
在抛物线![]() 上,且线段
上,且线段![]() 的中点恰在
的中点恰在![]() 轴上,
轴上,![]() 的面积为8.若抛物线
的面积为8.若抛物线![]() 上存在点
上存在点![]() 使得
使得![]() ,则实数
,则实数![]() 的最大值为( )
的最大值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ka﹣x(k,a为常数,a>0且a≠1)的图象过点A(0,1),B(3,8).
(1)求函数f(x)的解析式;
(2)若函数g(x)= ![]() 是奇函数,求b的值;
是奇函数,求b的值;
(3)在(2)的条件下判断函数g(x)的单调性,并用定义证明你的结论;
(4)解不等式g(3x)+g(x﹣3﹣x2)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 中,
中, ![]() 是
是![]() 的中点,
的中点, ![]() ,其周长为
,其周长为![]() ,若点
,若点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
(1)建立合适的平面直角坐标系,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若![]() 是射线
是射线![]() 上不同两点,
上不同两点, ![]() ,过点
,过点![]() 的直线与
的直线与![]() 交于
交于![]() ,直线
,直线![]() 与
与![]() 交于另一点
交于另一点![]() .证明:
.证明: ![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com