
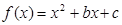 的图象过点
的图象过点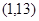 ,且函数对称轴方程为
,且函数对称轴方程为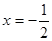 .
.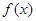 的解析式;
的解析式;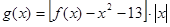 ,求
,求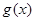 在区间
在区间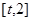 上的最小值
上的最小值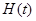 ;
;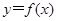 的图象上是否存在这样的点,使它的横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
的图象上是否存在这样的点,使它的横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.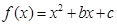 的对称轴方程为
的对称轴方程为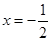 ,∴
,∴ 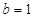 . ………… 2分
. ………… 2分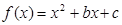 的图象过点(1,13),∴
的图象过点(1,13),∴ 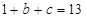 ,∴
,∴ 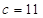 .
.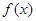 的解析式为
的解析式为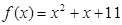 . ………………………………………… 4分
. ………………………………………… 4分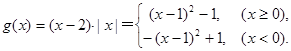 ……………………… 6分
……………………… 6分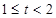 ,
,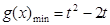 ;
;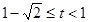 ,
,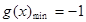 ;
;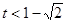 ,
,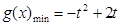 .……………………………… 9分
.……………………………… 9分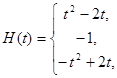
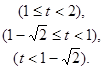 ……………………………………… 10分
……………………………………… 10分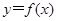 的图象上存在符合要求的点,设为
的图象上存在符合要求的点,设为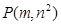 ,其中
,其中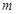 为正整数,
为正整数,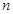 为自然数,则
为自然数,则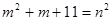 , ……………………………………… 11分
, ……………………………………… 11分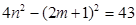 , 即
, 即 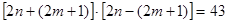 .
. 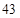 是质数,且
是质数,且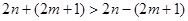 ,又
,又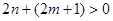 ,
,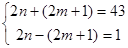 , 解得:
, 解得: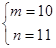 .…………………………… 13分
.…………………………… 13分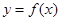 的图象上存在符合要求的点,它的坐标为
的图象上存在符合要求的点,它的坐标为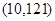 .………… 14分
.………… 14分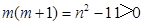 的偶数,∴
的偶数,∴ 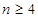 的奇数
的奇数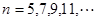 验证得,当
验证得,当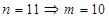 时符合
时符合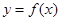 的图象上存在符合要求的点,它的坐标为
的图象上存在符合要求的点,它的坐标为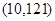 .………… 14分
.………… 14分

 一课一练课时达标系列答案
一课一练课时达标系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com