【答案】
分析:①因为原命题的逆命题与其否命题是互为逆否命题,是等价命题,即可判断出;
②方程

的图象表示双曲线的充要条件是(2-k)(k-1)<0,解得即可判断出;
③可知M(2,4)在抛物线y
2=8x上,因此过此点的切线和对称轴(x轴)平行的直线都与抛物线有且只有一个公共点,即可判断出;
④圆x
2+y
2=4的圆心(0,0)到直线4x-3y+5=0的距离d=

=1,而半径r=2,因此与此直线平行且与圆相切的其中一条切线满足条件,与此直线平行且距离为1的与圆相交的直线满足条件,故圆x
2+y
2=4上恰有三个点到直线4x-3y+5=0的距离为1,正确.
解答:解:①因为原命题的逆命题与其否命题是互为逆否命题,因此如果一个命题的逆命题为真命题,那么它的否命题一定是真命题,正确;
②方程

的图象表示双曲线的充要条件是(2-k)(k-1)<0,解得k<1或k>2,因此正确;
③可知M(2,4)在抛物线y
2=8x上,因此过此点的切线和对称轴(x轴)平行的直线都与抛物线有且只有一个公共点,故过点M(2,4)作与抛物线y
2=8x只有一个公共点的直线l有两条,不正确;
④圆x
2+y
2=4的圆心(0,0)到直线4x-3y+5=0的距离d=

=1,而半径r=2,因此与此直线平行且与圆相切的其中一条切线满足条件,与此直线平行且距离为1的与圆相交的直线满足条件,故圆x
2+y
2=4上恰有三个点到直线4x-3y+5=0的距离为1,正确.
综上可知:只有①②④正确.
故答案为①②④.
点评:本题综合考查了命题之间的关系、表示双曲线的充要条件、直线与抛物线的交点问题、直线与圆的交点问题等基础知识,考查了分析问题和解决问题的能力、推理能力和计算能力.

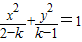 的图象表示双曲线的充要条件是k<1或k>2.
的图象表示双曲线的充要条件是k<1或k>2. 的图象表示双曲线的充要条件是(2-k)(k-1)<0,解得即可判断出;
的图象表示双曲线的充要条件是(2-k)(k-1)<0,解得即可判断出; =1,而半径r=2,因此与此直线平行且与圆相切的其中一条切线满足条件,与此直线平行且距离为1的与圆相交的直线满足条件,故圆x2+y2=4上恰有三个点到直线4x-3y+5=0的距离为1,正确.
=1,而半径r=2,因此与此直线平行且与圆相切的其中一条切线满足条件,与此直线平行且距离为1的与圆相交的直线满足条件,故圆x2+y2=4上恰有三个点到直线4x-3y+5=0的距离为1,正确. 的图象表示双曲线的充要条件是(2-k)(k-1)<0,解得k<1或k>2,因此正确;
的图象表示双曲线的充要条件是(2-k)(k-1)<0,解得k<1或k>2,因此正确; =1,而半径r=2,因此与此直线平行且与圆相切的其中一条切线满足条件,与此直线平行且距离为1的与圆相交的直线满足条件,故圆x2+y2=4上恰有三个点到直线4x-3y+5=0的距离为1,正确.
=1,而半径r=2,因此与此直线平行且与圆相切的其中一条切线满足条件,与此直线平行且距离为1的与圆相交的直线满足条件,故圆x2+y2=4上恰有三个点到直线4x-3y+5=0的距离为1,正确.
