D
分析:由已知中f(x)是连续的偶函数,且当x>0时,f(x)是单调函数,我们易得满足
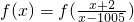
时,x=

或-x=

,将分式方程转化为整式方程后,利用韦达定理,易得到答案.
解答:∵f(x)是连续的偶函数,且当x>0时,f(x)是单调函数,
∴当
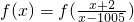
时
x=

或-x=

即x
2-1006x-2=0或x
2-1004x+2=0
由韦达定理得:
x
1+x
2=1006,x
3+x
4=1004
即满足
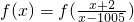
的所有x之和为1006+1004=2010
故选D
点评:本题考查的知识点是根的存在性及根的个数判断,其中根据函数奇偶性及单调性我们判断出满足
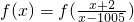
时,x=

或-x=

,是解答本题的关键.

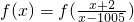 的所有x之和为
的所有x之和为