
分析 把${(x+\frac{1}{x})}^{6}$按照二项式定理展开,可得展开式中x3的系数.
解答 解:由于$(2x-1){(\frac{1}{x}+x)^6}$=(2x-1)•(${C}_{6}^{0}$•${(\frac{1}{x})}^{6}$+${C}_{6}^{1}$•${(\frac{1}{x})}^{4}$+${C}_{6}^{2}$•${(\frac{1}{x})}^{2}$+${C}_{6}^{3}$+${C}_{6}^{4}$•x2+${C}_{6}^{5}$•x4+${C}_{6}^{6}$•x6 ),
∴x3的系数为2${C}_{6}^{4}$=30,
故答案为:30.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
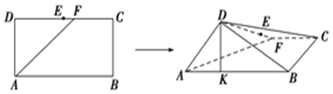 如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点,现将△AFD沿AF折起,使平面ABD⊥平面ABCF.在平面ABD内过点D作DK⊥AB,K为垂足,设AK=t,则t的取值范围是( )
如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点,现将△AFD沿AF折起,使平面ABD⊥平面ABCF.在平面ABD内过点D作DK⊥AB,K为垂足,设AK=t,则t的取值范围是( )| A. | ($\frac{1}{2}$,2) | B. | ($\frac{1}{2}$,1) | C. | ($\frac{\sqrt{3}}{2}$,2) | D. | ($\frac{\sqrt{3}}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
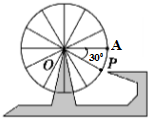 如图所示,一个半径为10m的摩天轮,轮子的底部在地面上2m处,如果此摩天轮按逆时针方向转动,每30s转一圈,且当摩天轮上某人经过点P处(∠POA=30°)时开始计时.
如图所示,一个半径为10m的摩天轮,轮子的底部在地面上2m处,如果此摩天轮按逆时针方向转动,每30s转一圈,且当摩天轮上某人经过点P处(∠POA=30°)时开始计时.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cosθ<tanθ<sinθ | B. | sinθ<cosθ<tanθ | C. | tanθ<sinθ<cosθ | D. | cosθ<sinθ<tanθ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
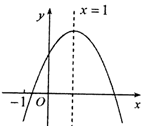 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;其中正确的结论为③④.(填序号)
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;其中正确的结论为③④.(填序号)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)∪(1,2) | B. | (-1,0)∪(1,+∞) | C. | (0,1)∪(2,+∞) | D. | (-∞,-1)∪(0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | (1,3) | B. | (-3,-1)∪(1,3) | C. | (-3,-1) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com