分析:(1)通过建立如图所示的空间直角坐标系,利用数量积
•=0?
⊥,即可证明AB
1⊥平面A
1BD;
(2)利用两个平面的法向量的夹角即可得到二面角.
解答:(1)
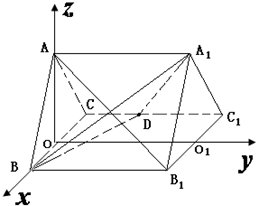
证明:取BC中点O,连接AO,∵△ABC为正三角形,∴AO⊥BC,
∵在正三棱柱ABC-A
1B
1C
1中,平面ABC⊥平面BCC
1B
1,∴AO⊥平面BCC
1B
1,
取B
1C
1中点为O
1,以O为原点,
,
,
的方向为x,y,z轴的正方向,建立空间直角坐标系,
则
B(2,0,0),D(-2,2.0),A1(0,4,2),A(0,0,2),B1(2,4,0).
∴
=(2,4,-2),
=(-4,2,0),
=(-2,4,2).
∵
•=-8+8+0=0,
•=-4+16-12=0.
∴
⊥,
⊥,
∴AB
1⊥面A
1BD.
(2)设平面A
1AD的法向量为
=(x,y,z),
=(-2,2,-2),(0,4,0).
⊥,⊥,
∴
,∴
,⇒
,
令z=1,得
=(-,0,1)为平面A
1AD的一个法向量,由(1)知AB
1⊥面A
1BD,
∴
为平面A
1AD的法向量,
cos<,>===-,
由图可以看出:二面角A-A
1D-B是锐角.
∴二面角A-A
1D-B的余弦值为
.
点评:熟练掌握:通过建立如图所示的空间直角坐标系的方法,利用数量积与垂直的关系证明线面垂直;利用两个平面的法向量的夹角得到二面角.

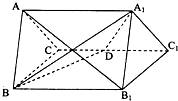 (2013•盐城二模)正三棱柱ABC-A1B1C1的所有棱长都为4,D为的CC1中点.
(2013•盐城二模)正三棱柱ABC-A1B1C1的所有棱长都为4,D为的CC1中点. 证明:取BC中点O,连接AO,∵△ABC为正三角形,∴AO⊥BC,
证明:取BC中点O,连接AO,∵△ABC为正三角形,∴AO⊥BC,
