Question

已知数列{a_n} 是公比为正数的等比数列，a₁=1，且3a₃是8a₁与a₅的等差中项，求数理{a_n} 的前n项和S_n．

Answer 1

解：设数列{a_n} 是公比为q（q＞0）
根据题意，3a₃是8a₁与a₅的等差中项，即6a₃=8a₁+a₅，
化简可得：6q²=8+q⁴，
解得q²=4或q²=2，
即q=2，q=，q=-2（舍去），
则q=2或q=，
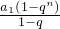
当q=2时，S_n==2ⁿ-1；
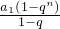
当q=时，S_n==（+1）（ⁿ-1）．
分析：先设数列{a_n} 是公比为q（q＞0），根据题意可得6a₃=8a₁+a₅，解可得q=2或q=，利用等比数列前n项和公式可得答案．
点评：本题考查等比数列的前n项和公式，涉及等差中项的性质，注意题干中“公比为正数”，求得的q=-2要舍去．