
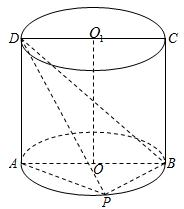
 如图,ABCD是底面半径为1的圆柱OO1的轴截面,P是下底面圆周上一点(异于A、B)
如图,ABCD是底面半径为1的圆柱OO1的轴截面,P是下底面圆周上一点(异于A、B)| 3 |
| 3 |
| ||
| 2 |
| π |
| 6 |


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:


查看答案和解析>>
科目:高中数学 来源: 题型:
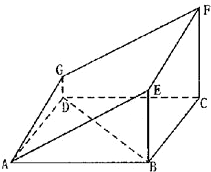 如图的多面体是底面为平行四边形的直四棱柱ABCD-A1B1C1D1,经平面AEFG所截后得到的图形.其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.
如图的多面体是底面为平行四边形的直四棱柱ABCD-A1B1C1D1,经平面AEFG所截后得到的图形.其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源:2010-2011学年黑龙江省鸡西市高三第五次月考数学理卷 题型:解答题
(本题满分12分)
如图的多面体是底面为平行四边形的直四棱柱ABCD—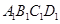 ,经平面AEFG所截后得到的图形.其中∠BAE=∠GAD=45°。AB=2AD=2.∠BAD=60。.
,经平面AEFG所截后得到的图形.其中∠BAE=∠GAD=45°。AB=2AD=2.∠BAD=60。.
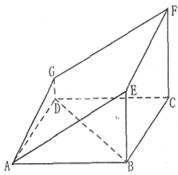
(I)求证:BD⊥平面ADG;
(Ⅱ)求平面AEFG与平面ABCD所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源:2008-2009学年上海市闵行区七宝中学高三(下)3月月考数学试卷(理科)(解析版) 题型:解答题
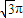 ,求二面角B-AD-P的大小.
,求二面角B-AD-P的大小.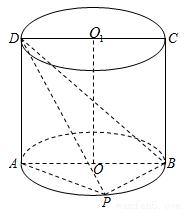
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com