已知一个直角三角形三个内角的正弦值成等比数列,则其中最小内角的正弦值是 .
【答案】
分析:设A、B为锐角,且A<B,C为直角,则sinC=1,sinB=cosA,由直角三角形三个内角的正弦值成等比数列,知sinA=sin
2B=cos
2A=1-sin
2A,设sinA=m,得m
2+m-1=0,由此能求出最小内角的正弦值.
解答:解:不妨设A、B为锐角,且A<B,C为直角,
则sinC=sin90°=1,sinB=cosA,
∵直角三角形三个内角的正弦值成等比数列,
∴
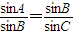
,
∴sinA=sin
2B=cos
2A=1-sin
2A,
设sinA=m,
则m=1-m
2,
m
2+m-1=0,
∴m=
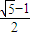
,或m=
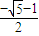
(舍).
所以最小内角的正弦值是
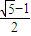
.
故答案为:
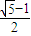
.
点评:本题考查三角函数与数列的综合运用,求直角三角形中最小角的正弦值.解题时要认真审题,注意等比数列的性质和应用,注意三角函数恒等式的灵活运用.

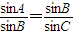 ,
,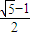 ,或m=
,或m=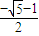 (舍).
(舍).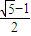 .
.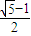 .
.
