练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    满足条件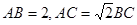的三角形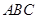的面积的最大值为        .

     

    【答案】

    【解析】解：设BC=x，则AC=  x，

    根据面积公式得S△ABC=1 /2 AB•BCsinB

    =1/ 2 ×2x  ，

    根据余弦定理得cosB=(AB2+BC2-AC2)/2AB•BC=[4+x2-( x)2] /4x =(4-x2) /4x ，

    代入上式得

    S△ABC=x 

    由三角形三边关系有 x+x＞2

    x+2＞ x   ，

    解得2  -2＜x＜2 +2．

    故当x=2 时，S△ABC取得最大值2

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

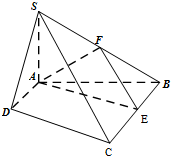    如图，四棱锥S-ABCD中，SA⊥平面ABCD，底面ABCD为直角梯形，AD∥BC，∠BAD=90°，且BC=2AD=2，AB=4，SA=3．
    （1）求证：平面SBC⊥平面SAB；
    （2）若E、F分别为线段BC、SB上的一点（端点除外），满足
    BF
    BS
    =
    BE
    BC
    =λ．（0＜λ＜1）
    ①求证：对于任意的λ∈（0，1），恒有SC∥平面AEF；
    ②是否存在λ，使得△AEF为直角三角形，若存在，求出所有符合条件的λ值；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    一块边长为10的正方形纸片，按如图所示将阴影部分裁下，然后将余下的四个全等的等腰三角形作为侧面制作一个正四棱锥S-ABCD（底面是正方形，顶点在底面的射影是底面中心的四棱锥）．
    （1）过此棱锥的高以及一底边中点F作棱锥的截面（如图），设截面三角形面积为y，求y的最大值及y取最大值时的x的值；
    （2）空间一动点P满足
    SP
    =a
    SA
    +b
    SB
    +c
    SC
    （a+b+c=1），在第（1）问的条件下，求|
    SP
    |    的最小值，并求取得最小值时a，b，c的值；
    （3）在第（1）问的条件下，设F是CD的中点，问是否存在这样的动点Q，它在此棱锥的表面（包含底面ABCD）运动，且FQ⊥AC？如果存在，计算其运动轨迹的长度，如果不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2015届福建省高一上学期期末考试数学试卷（解析版） 题型：解答题

    （本小题满分14分）

    如图，四棱锥S－ABCD中，SA⊥平面ABCD，底面ABCD为直角梯形，AD∥BC，∠BAD=90 ，且BC=2AD=2，AB=4，SA=3.

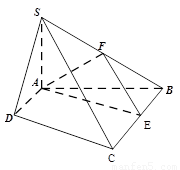
    （1）求证：平面SBC⊥平面SAB；

    （2）若E、F分别为线段BC、SB上的一点（端点除外），满足.（）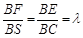

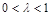    ①求证：对于任意的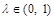，恒有SC∥平面AEF；

    ②是否存在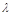，使得△AEF为直角三角形，若存在，求出所有符合条件的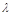值；若不存在，说明理由.

     

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年四川省成都市树德中学高二（上）期中数学试卷（理科）（解析版） 题型：解答题

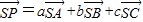    一块边长为10的正方形纸片，按如图所示将阴影部分裁下，然后将余下的四个全等的等腰三角形作为侧面制作一个正四棱锥S-ABCD（底面是正方形，顶点在底面的射影是底面中心的四棱锥）．
    （1）过此棱锥的高以及一底边中点F作棱锥的截面（如图），设截面三角形面积为y，求y的最大值及y取最大值时的x的值；
    （2）空间一动点P满足（a+b+c=1），在第（1）问的条件下，求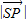的最小值，并求取得最小值时a，b，c的值；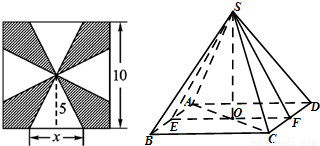
    （3）在第（1）问的条件下，设F是CD的中点，问是否存在这样的动点Q，它在此棱锥的表面（包含底面ABCD）运动，且FQ⊥AC？如果存在，计算其运动轨迹的长度，如果不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年福建省福州市文博中学高一（上）期末数学试卷（解析版） 题型：解答题

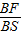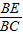    如图，四棱锥S-ABCD中，SA⊥平面ABCD，底面ABCD为直角梯形，AD∥BC，∠BAD=90°，且BC=2AD=2，AB=4，SA=3．
    （1）求证：平面SBC⊥平面SAB；
    （2）若E、F分别为线段BC、SB上的一点（端点除外），满足==λ．（0＜λ＜1）
    ①求证：对于任意的λ∈（0，1），恒有SC∥平面AEF；
    ②是否存在λ，使得△AEF为直角三角形，若存在，求出所有符合条件的λ值；若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案