分析:(1)求证:直线C1P∥平面AB1C,取B1C中点Q,连接AQ,只需证明PC1∥AQ即可;
(2)求异面直线AA1与B1P所成角的余弦值,法一:作出异面直线所成的角,直接解三角形即可;法二:利用空间直角坐标系,求出相关向量,求数量积即可.
解答: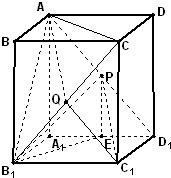
解:(1)证明:取B
1C中点Q,连接AQ,QC
1,
则QC
1∥AP且QC
1=AP,所以四边形APC
1Q是平行四边形,所以PC
1∥AQ,
又AQ?平面AB
1C,C
1P?平面AB
1C,所以直线C
1P∥平面AB
1C
(2)解法一:过点P作PE⊥A
1D
1,垂足为E,连接B
1E(如图),
则PE∥AA
1,∴∠B
1PE是异面直线AA
1与B
1P所成的角.
在 Rt△AA
1D
1中∵∠AD
1A
1=60°
∴∠A
1AD
1=30°
∴
A1B1=A1D1=AD1=2,
A1E=A1D1=1,
∴
B1E==.
又
PE=AA1=.
∴在 Rt△B
1PE中,
B1P==2cos∠B1PE===.
∴异面异面直线AA
1与B
1P所成角的余弦值为
.
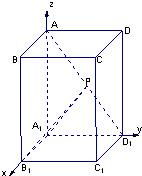
解法二:以A
1为原点,A
1B
1所在的直线为x轴建立空间直角坐标系如图示,
则A
1(0,0,0),
A(0,0,2),B
1(2,0,0),
P(0,1,),
∴
=(0,0,2),
=(-2,1,)∴
cos<,>==
=.
∴异面异面直线AA
1与B
1P所成角的余弦值为
.
点评:本题考查直线与平面平行的判定,异面直线所成的角,考查学生逻辑思维能力,空间想象能力,是中档题.

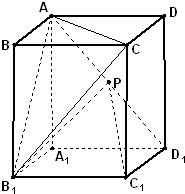 如图,已知ABCD-A1B1C1D1是底面为正方形的长方体,∠AD1A1=60°,AD1=4,P为AD1的中点,(1)求证:直线C1P∥平面AB1C;(2)求异面直线AA1与B1P所成角的余弦值.
如图,已知ABCD-A1B1C1D1是底面为正方形的长方体,∠AD1A1=60°,AD1=4,P为AD1的中点,(1)求证:直线C1P∥平面AB1C;(2)求异面直线AA1与B1P所成角的余弦值.  解:(1)证明:取B1C中点Q,连接AQ,QC1,
解:(1)证明:取B1C中点Q,连接AQ,QC1, 解法二:以A1为原点,A1B1所在的直线为x轴建立空间直角坐标系如图示,
解法二:以A1为原点,A1B1所在的直线为x轴建立空间直角坐标系如图示,

 互动英语系列答案
互动英语系列答案
 (2012•汕头二模)如图,已知ABCD-A1B1C1D1是底面边长为1的正四棱柱,
(2012•汕头二模)如图,已知ABCD-A1B1C1D1是底面边长为1的正四棱柱, 如图,已知ABCD是正方形,DE⊥平面ABCD,BF⊥平面ABCD,且AB=FB=2DE.
如图,已知ABCD是正方形,DE⊥平面ABCD,BF⊥平面ABCD,且AB=FB=2DE. (2005•普陀区一模)如图,已知ABCD和A1B1C1D1都是正方形,且AB∥A1B1,AA1=BB1=CC1=DD1,若将图中已作出的线段的两个端点分别作为向量的始点和终点所形成的不相等的向量的全体构成集合M,则从集合M中任取两个向量恰为平行向量的概率是
(2005•普陀区一模)如图,已知ABCD和A1B1C1D1都是正方形,且AB∥A1B1,AA1=BB1=CC1=DD1,若将图中已作出的线段的两个端点分别作为向量的始点和终点所形成的不相等的向量的全体构成集合M,则从集合M中任取两个向量恰为平行向量的概率是