方程x2-2ax+4=0的两根均大于1,则实数a的范围是 ________.
2≤a<

.
分析:方法一:先设方程x
2-2ax+4=0的两根为x
1、x
2,方程x
2-2ax+4=0的两根均大于1,故两根之和大于2,两根与1的差的乘积大于0.将此两不等式转化为关于参数a的不等式,解出a的范围即所求.
方法二:由题设方程相应的函数与x轴的两个交点都在直线x=1的右侧,且开口方向向上,对称轴大于1,由此可以将这些特征转化为
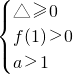
,解之即得a的范围
解答:解法一:利用韦达定理,设方程x
2-2ax+4=0的两根为x
1、x
2,
则

∴
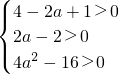
解之得 2≤a<

.
解法二:利用二次函数图象的特征,设f(x)=x
2-2ax+4,
则
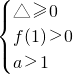
,

解之得2≤a<

.
故应填 2≤a<

点评:本题考查二次方程根的分布知识,方法一利用根与系数的关系转化,方法二利用函数图象的特征进行转化,这是解此类题时常用的两种方法.

 .
.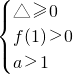 ,解之即得a的范围
,解之即得a的范围 ∴
∴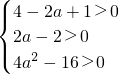
 .
.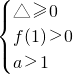 ,
, 解之得2≤a<
解之得2≤a< .
.

