
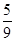
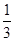 },算出事件对应的集合表示的面积,根据几何概型概率公式得到结果.解:设两人到达约会地点的时刻分别为x,y,依题意,必须满足|x-y|≤
},算出事件对应的集合表示的面积,根据几何概型概率公式得到结果.解:设两人到达约会地点的时刻分别为x,y,依题意,必须满足|x-y|≤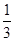 才能相遇.我们把他们到达的时刻分别作为横坐标和纵坐标,于是两人到达的时刻均匀地分布在一个边长为1的正方形Ⅰ内,如图所示,而相遇现象则发生在阴影区域G内,即甲、乙两人的到达时刻(x,y)满足|x-y|≤
才能相遇.我们把他们到达的时刻分别作为横坐标和纵坐标,于是两人到达的时刻均匀地分布在一个边长为1的正方形Ⅰ内,如图所示,而相遇现象则发生在阴影区域G内,即甲、乙两人的到达时刻(x,y)满足|x-y|≤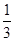 ,所以两人相遇的概率为区域G与区域Ⅰ的面积之比:
,所以两人相遇的概率为区域G与区域Ⅰ的面积之比: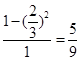


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com