
【题目】如图,在直四棱柱![]() 中,底面
中,底面![]() 为等腰梯形,
为等腰梯形,![]() ,
,![]() ,且
,且![]() 为棱
为棱![]() 中点,
中点,![]() 为棱
为棱![]() 中点.
中点.
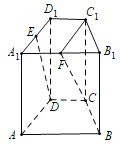
(1)证明:![]() 平面
平面![]() ;
;
(2)求锐二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】已知![]() ,直线
,直线![]() 与函数
与函数![]() 的图象在
的图象在![]() 处相切,设
处相切,设![]() ,若在区间[1,2]上,不等式
,若在区间[1,2]上,不等式![]() 恒成立.则实数m( )
恒成立.则实数m( )
A. 有最大值![]() B. 有最大值e C. 有最小值e D. 有最小值
B. 有最大值e C. 有最小值e D. 有最小值![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定椭圆C:![]() (
(![]() ),称圆心在原点O,半径为
),称圆心在原点O,半径为![]() 的圆是椭圆C的“卫星圆”.若椭圆C的离心率
的圆是椭圆C的“卫星圆”.若椭圆C的离心率![]() ,点
,点![]() 在C上.
在C上.
(1)求椭圆C的方程和其“卫星圆”方程;
(2)点P是椭圆C的“卫星圆”上的一个动点,过点P作直线![]() ,
,![]() 使得
使得![]()
![]()
![]() ,与椭圆C都只有一个交点,且
,与椭圆C都只有一个交点,且![]() ,
,![]() 分别交其“卫星圆”于点M,N,证明:弦长
分别交其“卫星圆”于点M,N,证明:弦长![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某书店今年5月上架10种新书,且它们的首月销量(单位:册)情况为:100,50,100,150,150,100,150,50,100,100,频率为概率,解答以下问题:
(1)若该书店打算6月上架某种新书,估计它首月销量至少为100册的概率;
(2)若某种最新出版的图书订购价为10元/册,该书店计划首月内按12元/册出售,第二个月起按8元/册降价出售,降价后全部存货可以售出.试确定,该书店订购该图书50册,100册,还是150册有利于获得更多利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,几何体![]() 中,
中,![]() ,
,![]() 均为边长为2的正三角形,且平面
均为边长为2的正三角形,且平面![]() 平面
平面![]() ,四边形
,四边形![]() 为正方形.
为正方形.
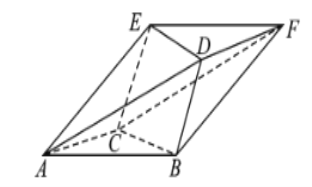
(1)若平面![]() 平面
平面![]() ,求证:平面
,求证:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 为
为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com