
点![]() 是边长为4的正方形
是边长为4的正方形![]() 的中心,点
的中心,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.沿对角线
的中点.沿对角线![]() 把正方形
把正方形![]() 折成直二面角D-AC-B.
折成直二面角D-AC-B.
(Ⅰ)求![]() 的大小;
的大小;
(Ⅱ)求二面角![]() 的大小.
的大小.
解法一:(Ⅰ)如图,过点E作EG⊥AC,垂足为G,过点F作FH⊥AC,垂足为H,则![]() ,
,![]() .
.
 | |||
 | |||
因为二面角D-AC-B为直二面角,
![]()
![]()
又在![]() 中,
中,![]() ,
,
![]() .
.
![]() .
.
(Ⅱ)过点G作GM垂直于FO的延长线于点M,连EM.
∵二面角D-AC-B为直二面角,∴平面DAC⊥平面BAC,交线为AC,又∵EG⊥AC,∴EG⊥平面BAC.∵GM⊥OF,由三垂线定理,得EM⊥OF.
∴![]() 就是二面角
就是二面角![]() 的平面角.
的平面角.
在Rt![]() EGM中,
EGM中,![]() ,
,![]() ,
,![]() ,
,
∴![]() .∴
.∴![]() .
.
所以,二面角![]() 的大小为
的大小为![]() .
.
 解法二:(Ⅰ)建立如图所示的直角坐标系O-xyz,
解法二:(Ⅰ)建立如图所示的直角坐标系O-xyz,
则![]() ,
,![]() .
.
![]() .
.
![]() .
.
(Ⅱ)设平面OEF的法向量为![]() .
.
由![]() 得
得
 解得
解得![]() .
.
所以,![]() .
.
又因为平面AOF的法向量为![]() ,
,
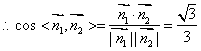 .∴
.∴![]() .
.
所以,二面角![]() 的大小为
的大小为![]()


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
| y2 |
| a2 |
| x2 |
| b2 |
| MP |
| PN |
查看答案和解析>>
科目:高中数学 来源:云南省期中题 题型:解答题
 是边长为4的正方形
是边长为4的正方形 的中心,点
的中心,点 ,
, 分别是
分别是 ,
,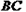 的中点.沿对角线
的中点.沿对角线 把正方形
把正方形 折成直二面角D-AC-B.
折成直二面角D-AC-B. 
 的大小;
的大小; 的正切值.
的正切值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com