
 如图,已知点C在圆O直径BE的延长线上,CA切圆O于点A,CD是∠ACB的平分线,交AE于点F,交AB于点D.
如图,已知点C在圆O直径BE的延长线上,CA切圆O于点A,CD是∠ACB的平分线,交AE于点F,交AB于点D.分析 (I)利用圆周角定理可得∠CAE=∠ABC,进而利用相似三角形的性质可得$\frac{CE}{CA}=\frac{AE}{AB}$,又角平分线的性质可得
$\frac{CE}{CA}=\frac{EF}{AF}$,从而解得$\frac{AE}{AB}=\frac{EF}{AF},即AE•AF=AB•EF$.
(Ⅱ)先求△ACF∽△BCD,利用相似三角形的性质可得$\frac{AC}{BC}=\frac{AF}{BD}=\frac{AD}{BD}=\frac{1}{2}$,从而可求BC,利用切割线定理即可解得CE的值.
解答 (本题满分为10分)
解:(I)证明:∵CA为圆O的切线,
∴∠CAE=∠ABC,
则△ACE∽△ACB,
∴$\frac{CE}{CA}=\frac{AE}{AB}$,
∵CF是∠ACB的平分线,
∴$\frac{CE}{CA}=\frac{EF}{AF}$,
∴$\frac{AE}{AB}=\frac{EF}{AF},即AE•AF=AB•EF$.…(5分)
(Ⅱ)解:∵CD是∠ACB的平分线,
∴∠ACF=∠DCB,
∵CA切圆O于点A,
∴∠CAF=∠ABC,
∴△ACF∽△BCD,
∴$\frac{AC}{BC}=\frac{AF}{BD}=\frac{AD}{BD}=\frac{1}{2}$,
∴BC=2AC=4,
∵CA为圆O的切线,
∴CA2=CE•CB,
∴CE=1.…(10分)
点评 本题主要考查了圆周角定理,相似三角形的性质,角平分线的性质,切割线定理的综合应用,考查了转化思想和数形结合思想的应用,考查学生分析解决问题的能力,属于中档题.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:选择题
| A. | S2 | B. | S61 | C. | S62 | D. | S63 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
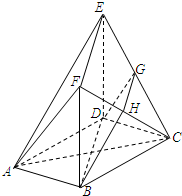 如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G和H分别是CE和CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G和H分别是CE和CF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{5}$) | B. | (0,$\frac{1}{3}$) | C. | ($\frac{1}{5}$,$\frac{1}{3}$) | D. | ($\frac{1}{3}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com