
| A. | S2 | B. | S61 | C. | S62 | D. | S63 |
分析 运用等差数列的定义可得,数列{a${\;}_{n}^{3}$}是首项为125,公差为-2的等差数列,运用等差数列的通项公式可得a${\;}_{n}^{3}$=125+(-2)(n-1)=127-2n,判断数列的单调性,即可得到所求和的最大值.
解答 解:由a${\;}_{n+1}^{3}$-a${\;}_{n}^{3}$=-2,a1=5,
可得数列{a${\;}_{n}^{3}$}是首项为125,公差为-2的等差数列,
可设bn=a${\;}_{n}^{3}$=125+(-2)(n-1)=127-2n,
由bn≥0,bn+1≤0,
即127-2n≥0,125-2n≤0,
解得62$\frac{1}{2}$≤n≤63$\frac{1}{2}$,
即有自然数n为63.
由等差数列{a${\;}_{n}^{3}$}为递减数列,
可得前63项均为正数,第64项起均为负数.
则前63项和最大.
故选:D.
点评 本题考查等差数列的定义和通项公式的求法,同时考查数列的和的最值,注意运用数列的单调性,属于中档题.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{11}$ | B. | $\frac{1}{10}$ | C. | 11 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
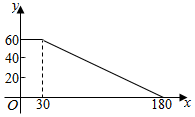 经观测发现在一般情况下,一过江大桥的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,函数v(x)的图象如图所示.
经观测发现在一般情况下,一过江大桥的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,函数v(x)的图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知点C在圆O直径BE的延长线上,CA切圆O于点A,CD是∠ACB的平分线,交AE于点F,交AB于点D.
如图,已知点C在圆O直径BE的延长线上,CA切圆O于点A,CD是∠ACB的平分线,交AE于点F,交AB于点D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| ξ | 1 | 2 | 3 |
| P | 0.3 | 0.1 | 0.6 |
| η | 1 | 2 | 3 |
| P | 0.3 | 0.4 | 0.3 |
| A. | 甲好于乙 | B. | 乙好于甲 | C. | 一样好 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com