
在平面斜坐标系 中
中 ,点
,点 的斜坐标定义为:“若
的斜坐标定义为:“若 (其中
(其中 分别为与斜坐标系的
分别为与斜坐标系的 轴,
轴, 轴同方向的单位向量),则点
轴同方向的单位向量),则点 的坐标为
的坐标为 ”.若
”.若 且动点
且动点 满足
满足 ,则点
,则点 在斜坐标系中的轨迹方程为( )
在斜坐标系中的轨迹方程为( )
A. B.
B.
C. D.
D.
科目:高中数学 来源:2016-2017学年甘肃省高一上学期第一次阶段考数学试卷(解析版) 题型:解答题
(重点班)我们知道对数函数 ,对任意
,对任意 ,都有
,都有 成立,若
成立,若 ,则当
,则当 时,
时, .参照对数函数的性质,研究下题:定义在
.参照对数函数的性质,研究下题:定义在 上的函数
上的函数 对任意
对任意 ,都有
,都有 ,并且当且仅当
,并且当且仅当 时,
时, 成立.
成立.
(1)设 ,求证:
,求证: ;
;
(2)设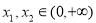 ,若
,若 ,比较
,比较 与
与 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年福建省高二文上学期10月考试数学试卷(解析版) 题型:选择题
若 ,则“
,则“ ”是“
”是“ ”的
”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2017届浙江温州中学高三10月高考模拟数学试卷(解析版) 题型:解答题
如图,已知平面
 平面
平面 ,
, 与
与 分别是棱长为1与2的正三角形,
分别是棱长为1与2的正三角形, //
// ,四边形
,四边形 为直角梯形,
为直角梯形, //
// ,
, ,点
,点 为
为 的重心,
的重心, 为
为 中点,
中点, .
.

(Ⅰ)当 时,求证:
时,求证: //平面
//平面 ;
;
(Ⅱ)若直线 与
与 所成角为
所成角为 ,试求二面角
,试求二面角 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源:2017届新疆生产建设兵团二中高三上月考二数学(理)试卷(解析版) 题型:解答题
选修4-5:不等式选讲
已知定义在 上的函数
上的函数 的最大值为
的最大值为 .
.
(1)试求 的值;
的值;
(2)若 ,且
,且 ,求证:
,求证: .
.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年四川省成都市高二文10月考数学试卷(解析版) 题型:解答题
如图1,已知四边形 为直角梯形,
为直角梯形, ,
, ,
, ,
, 为等边三角形,
为等边三角形, ,
, ,如图2,将
,如图2,将 ,
, 分别沿
分别沿 折起,使得平面
折起,使得平面 平面
平面 ,平面
,平面 平面
平面 ,连接
,连接 ,设
,设 为
为 上任意一点.
上任意一点.

(1)证明: 平面
平面 ;
;
(2)若 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年四川成都经济技术开发区实验高二文10月考数学卷(解析版) 题型:选择题
△ABC的内角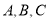 的对边分别为
的对边分别为 ,若
,若 成等比数列,且
成等比数列,且 ,则
,则
A.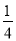 B.
B. C.
C.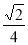 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com