
已知椭圆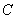 的中心在原点,焦点在
的中心在原点,焦点在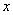 轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为
轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为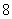 的正方形(记为
的正方形(记为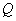 )
)
(1)求椭圆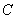 的方程
的方程
(2)设点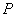 是直线
是直线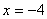 与
与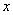 轴的交点,过点
轴的交点,过点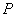 的直线
的直线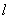 与椭圆
与椭圆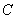 相交于
相交于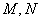 两点,当线段
两点,当线段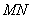 的中点落在正方形
的中点落在正方形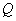 内(包括边界)时,求直线
内(包括边界)时,求直线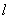 斜率的取值范围
斜率的取值范围
解: (Ⅰ)依题意,设椭圆C的方程为=1(a>b>0),焦距为2c,
由题设条件知,a2=8,b=c, 所以b2=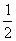 a2=4
a2=4
故椭圆C的方程为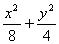 =1 (4分)
=1 (4分)
 (Ⅱ)椭圆C的左准线方程为x=-4,所以点P的坐标为(-4,0),
(Ⅱ)椭圆C的左准线方程为x=-4,所以点P的坐标为(-4,0),
显然直线l的斜率k存在,所以直线的方程为y=k(x+4)。
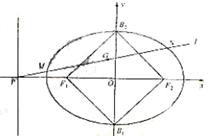
如图,设点M,N的坐标分别为(x1,y1),(x2,y2),线段MN的
中点为G(x0,y0),
由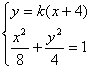
得(1+2k2)x2+16k2x+32k2-8=0 ① (6分)
由D=(16k2)2-4(1+2k2)(32k2-8)>0
解得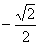 <k<
<k<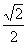 ② (7分)
② (7分)
因为x1,x2是方程①的两根,所以x1+x2=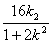 ,
,
于是x0=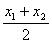 =
=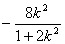 ,y0=k(x0+4)=
,y0=k(x0+4)= (8分)
(8分)
∵x0=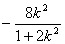 ≤0,所以点G不可能在y轴的右边. (9分)
≤0,所以点G不可能在y轴的右边. (9分)
又直线F1B2,F1B1方程分别为y=x+2,y=-x-2
所以点G在正方形Q内(包括边界)的充要条件为
 即
即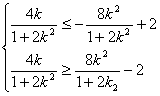 (10分)
(10分)
解得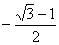 ≤k≤
≤k≤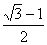 ,此时②也成立. (12分)
,此时②也成立. (12分)
故直线l斜率的取值范围是[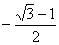 ,
,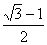 ]. (13分)
]. (13分)


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
以下茎叶图记录了甲乙两组各五名学生在一次英语听力测试中的成绩
(单位:分)
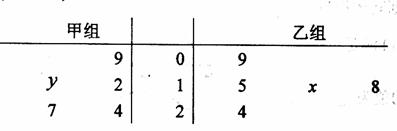
已知甲组数据的中位数为15,乙组数据的平均数为16.8,则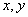 的值分别为
的值分别为
A. 5,2 B.5,5 C. 8,5 D.8,8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com