练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数y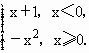＝试设计一个算法，输入x的值，求对应的函数值．

    答案：
    解析：

    　　解：算法步骤如下：

    　　第一步：输入x的值；

    　　第二步：当x＜0时，计算y＝x＋1，否则执行第三步；

    　　第三步：计算y＝－x2；

    　　第四步：输出y．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：甘肃省兰州一中2009－2010学年度高三第一学期期中考试(数学文) 题型：013

    已知函数y＝Asin()在一个周期内，当x＝时，y取得最大值是2；当x＝0时，y取得最小值是－2，则此函数的表达式为

    [　　]
    A．

    y＝2sin(3x－)

    B．

    y＝2sin(3x＋)

    C．

    y＝2sinx

    D．

    y＝sin(3x－)

    查看答案和解析>>

    科目：高中数学 来源：2014届山东省高二上学期10月月考数学试卷（解析版） 题型：解答题

    (本小题满分12分)已知函数y＝|cosx＋sinx|.

    (1)画出函数在x∈[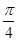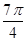－，]上的简图；

    (2)写出函数的最小正周期和在[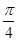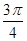－，]上的单调递增区间；试问：当x在R上取何值

    时，函数有最大值？最大值是多少？

    (3)若x是△ABC的一个内角，且y2＝1，试判断△ABC的形状．

     

    查看答案和解析>>

    科目：高中数学 来源：2012年人教A版高中数学必修四1.5函数的图象练习卷（一）（解析版） 题型：解答题

    已知函数y＝Asin(ωx＋φ)(A>0、ω>0，|φ|<)的图象的一个最高点为(2,2)，由这个最高点到相邻最低点，图象与x轴交于(6,0)点，试求这个函数的解析式．

     

    查看答案和解析>>

    科目：高中数学 来源：新课标高三数学三角函数专项训练（河北） 题型：解答题

    已知函数y＝|cosx＋sinx|.

    (1)画出函数在x∈[－，]的简图；

    (2)写出函数的最小正周期和单调递增区间；试问：当x为何值时，函数有最大值？最大值是多少？

    (3)若x是△ABC的一个内角，且y2＝1，试判断△ABC的形状．

     

    查看答案和解析>>

    同步练习册答案