
某单位从一所学校招收某类特殊人才.对 位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
例如,表中运动协调能力良好且逻辑思维能力一般的学生有 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这 位参加测试的学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生的概率为
位参加测试的学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生的概率为 .
.
(1)求 ,
, 的值;
的值;
(2)从参加测试的 位学生中任意抽取
位学生中任意抽取 位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率;
位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率;
(3)从参加测试的 位学生中任意抽取
位学生中任意抽取 位,设运动协调能力或逻辑思维能力优秀的学生人数为
位,设运动协调能力或逻辑思维能力优秀的学生人数为 ,求随机变量
,求随机变量 的分布列及其数学期望
的分布列及其数学期望 .
.
(1) ,
,  ;(2)
;(2) ;(3)所以
;(3)所以 的分布列为
的分布列为
0 1 2 



 .
.
解析试题分析:(1)求 ,
, 的值,由题意,从这
的值,由题意,从这 位参加测试的学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生的概率为
位参加测试的学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生的概率为 ,而由表中数据可知,运动协调能力或逻辑思维能力优秀的学生共有
,而由表中数据可知,运动协调能力或逻辑思维能力优秀的学生共有 人,可由
人,可由 ,解出
,解出 的值,从而得
的值,从而得 的值;(2)由题意,从
的值;(2)由题意,从 人中任意抽取
人中任意抽取 人的方法数为
人的方法数为 ,而至少有一位运动协调能力或逻辑思维能力优秀的学生的对立事件是,没有取到运动协调能力或逻辑思维能力优秀的学生,而没有取到运动协调能力或逻辑思维能力优秀的学生的方法数为
,而至少有一位运动协调能力或逻辑思维能力优秀的学生的对立事件是,没有取到运动协调能力或逻辑思维能力优秀的学生,而没有取到运动协调能力或逻辑思维能力优秀的学生的方法数为 ,由古典概型,可求出没有运动协调能力或逻辑思维能力优秀的学生的概率,从而得所求的概率;(3)由题意得
,由古典概型,可求出没有运动协调能力或逻辑思维能力优秀的学生的概率,从而得所求的概率;(3)由题意得 的可能取值为
的可能取值为 ,由古典概型,分别求出它们的概率,得随机变量
,由古典概型,分别求出它们的概率,得随机变量 的分布列,从而得数学期望
的分布列,从而得数学期望 .
.
试题解析:(I)设事件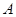 :从
:从 位学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生.由题意可知,运动协调能力或逻辑思维能力优秀的学生共有
位学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生.由题意可知,运动协调能力或逻辑思维能力优秀的学生共有 人.
人.
则 .解得
.解得  .所以
.所以 . 4分
. 4分
(2)设事件 :从
:从 人中任意抽取
人中任意抽取 人,至少有一位运动协调能力或逻辑思维能力优秀的学生.
人,至少有一位运动协调能力或逻辑思维能力优秀的学生.
由题意可知,至少有一项能力测试优秀的学生共有 人.
人.
则 . 7分
. 7分
(3) 的可能取值为
的可能取值为 ,
, ,
, .
. 位学生中运动协调能力或逻辑思维能力优秀的学生人数为
位学生中运动协调能力或逻辑思维能力优秀的学生人数为 人.
人.
所以 ,
, ,
, .
.
所以 的分布列为
的分布列为
所以,
0 1 2 



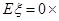





 . 13分
. 13分
考点:古典概型,分布列,数学期望.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源: 题型:解答题
某中学在高一开设了数学史等4门不同的选修课,每个学生必须选修,且只能从中选一门.该校高一的3名学生甲、乙、丙对这4门不同的选修课的兴趣相同.
(1)求3个学生选择了3门不同的选修课的概率;
(2)求恰有2门选修课这3个学生都没有选择的概率;
(3)设随机变量X为甲、乙、丙这三个学生选修数学史这门课的人数,求X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)求在一次游戏中,①摸出3个白球的概率,②获奖的概率;
(2)求在两次游戏中获奖次数X的分布列及数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,将得到的点数分别记为 .
.
(1)求直线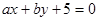 与圆
与圆 相切的概率;
相切的概率;
(2)将 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对某电子元件进行寿命追踪调查,所得情况如右频率分布直方图.
(1)图中纵坐标 处刻度不清,根据图表所提供的数据还原
处刻度不清,根据图表所提供的数据还原 ;
;
(2)根据图表的数据按分层抽样,抽取 个元件,寿命为
个元件,寿命为 之间的应抽取几个;
之间的应抽取几个;
(3)从(2)中抽出的寿命落在 之间的元件中任取
之间的元件中任取 个元件,求事件“恰好有一个寿命为
个元件,求事件“恰好有一个寿命为 ,一个寿命为
,一个寿命为 ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知 、
、 两个盒子中分别装有标记为
两个盒子中分别装有标记为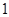 ,
, ,
, ,
, 的大小相同的四个小球,甲从
的大小相同的四个小球,甲从 盒中等可能地取出
盒中等可能地取出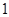 个球,乙从
个球,乙从 盒中等可能地取出
盒中等可能地取出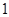 个球.
个球.
(1)用有序数对 表示事件“甲抽到标号为
表示事件“甲抽到标号为 的小球,乙抽到标号为
的小球,乙抽到标号为 的小球”,试写出所有可能的事件;
的小球”,试写出所有可能的事件;
(2)甲、乙两人玩游戏,约定规则:若甲抽到的小球的标号比乙大,则甲胜;反之,则乙胜.你认为此规则是否公平?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
若一批白炽灯共有10000只,其光通量X服从正态分布,其正态分布密度函数是f(x)= ,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数.
,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数.
(1)(203,215);(2)(191,227).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某超市在节日期间进行有奖促销,凡在该超市购物满400元的顾客,将获得一次摸奖机会,规则如下:奖盒中放有除颜色外完全相同的1个红球,1个黄球,1个白球和1个黑球.顾客不放回的每次摸出1个球,若摸到黑球则停止摸奖,否则就继续摸球.规定摸到红球奖励20元,摸到白球或黄球奖励10元,摸到黑球不奖励.
(1)求1名顾客摸球2次停止摸奖的概率;
(2)记 为1名顾客摸奖获得的奖金数额,求随机变量
为1名顾客摸奖获得的奖金数额,求随机变量 的分布律和数学期望.
的分布律和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
从1,2,3,4,5,6中不放回地随机抽取四个数字,记取得的四个数字之和除以4的余数为 ,除以3的余数为
,除以3的余数为
(1)求X=2的概率;
(2)记事件 为事件
为事件 ,事件
,事件 为事件
为事件 ,判断事件
,判断事件 与事件
与事件 是否相互独立,并给出证明.
是否相互独立,并给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com