
如下图,在△ABC中,BC边的中点M为(-![]() ,
,![]() ),直线AC的方程为x+1=0,直线AB的方程为x+y-1=0,求直线BC的方程.
),直线AC的方程为x+1=0,直线AB的方程为x+y-1=0,求直线BC的方程.

|
解法一:利用两点式. 设B(a,1-a)、C(-1,b), 则 ∴ ∴BC的方程为 解法二:利用点斜式. 设直线BC的方程为y- 由 ∴由中点坐标公式,得 ∴直线BC的方程为3x+y+7=0. 解法三:利用两点式. 作MD∥AC交AB于D,则点D(- ∵A(-1,2),∴B(-4,5). ∴由点M、B的坐标可得,直线BC的方程为3x+y+7=0. |
|
确定直线的方程需要两个条件,本题已经给出直线BC经过M点,所以只要求得点B(或C)的坐标或直线BC的斜率就可以了. |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2012-2013学年山东省淄博一中高一上学期期末考试数学试卷(带解析) 题型:单选题
如下图,在△ABC中,设 =
= ,
,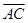 =
= ,AP的中点为Q,BQ的中点为R,CR的中点为P,若
,AP的中点为Q,BQ的中点为R,CR的中点为P,若 =m
=m +n
+n ,则
,则 ( )
( ) 
A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:2015届山东省高一上学期期末考试数学试卷(解析版) 题型:选择题
如下图,在△ABC中,设 =
= ,
, =
= ,AP的中点为Q,BQ的中点为R,CR的中点为P,若
,AP的中点为Q,BQ的中点为R,CR的中点为P,若 =m
=m +n
+n ,则
,则 ( )
( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com