
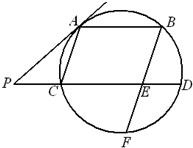
如图,AB、CD是⊙O的两条平行切线,B、D为切点,AC为⊙O的切线,切点为E.过A作AF⊥CD,F为垂足.

(1)求证:四边形ABDF是矩形;
(2)若AB=4,CD=9,求⊙O的半径.
(1)连结OB,并作BO的延长线,推出OB⊥AB;根据AB∥CD,
推出BD为⊙O直径,又∵AF⊥CD,∴四边形ABDF是矩形。
(2)⊙O的半径长为6 。
【解析】
试题分析:(1)连结OB,并作BO的延长线,

∵AB切⊙O于B,∴OB⊥AB
∵AB∥CD,∴BO⊥CD,∴BO经过D点
∴BD为⊙O直径
又∵AF⊥CD,∴四边形ABDF是矩形 5分
(2)在RtΔACF中,
由切线长定理得 AB=AE, CE=CD
∴AC=AE+CE=AB+CD=13,CF=CD-DF=CD-AB=5
∴AF=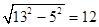 ,从而OB=6
,从而OB=6
即⊙O的半径长为6 10分
考点: 本题主要考查圆的几何性质,切线长定理,弦切角定理。
点评:中档题,作为选考内容,题目的难度往往不大,突出对基础知识的考查。


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
 如图,AB、CD是圆的两条平行弦,BE∥AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
如图,AB、CD是圆的两条平行弦,BE∥AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2008•佛山一模)(几何证明选讲)如图,AB、CD是圆O的两条弦,且AB是线段CD的中垂线,已知AB=6,CD=2
(2008•佛山一模)(几何证明选讲)如图,AB、CD是圆O的两条弦,且AB是线段CD的中垂线,已知AB=6,CD=2| 5 |
| 30 |
| 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (1)不等式|2x-1|-|x+2|≥1的解集
(1)不等式|2x-1|-|x+2|≥1的解集| 2 |
| 3 |
| 2 |
| 3 |
|
| 2a |
| 3 |
| 9a |
| 8 |
| 9a |
| 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com