
 在Rt△ABC内有一内接正方形,它的一条边在斜边BC上,如图所示.
在Rt△ABC内有一内接正方形,它的一条边在斜边BC上,如图所示.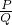 的最小值.
的最小值. ,AC=atanθ
,AC=atanθ 
 =BD+DE+EC=x+xcotθ+xtanθ
=BD+DE+EC=x+xcotθ+xtanθ  =
=
 AB×AC=
AB×AC= a2tanθ
a2tanθ 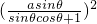 .
.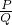 =
= ×
×
 +
+ sinθcosθ+1
sinθcosθ+1 
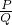 =1+
=1+ +
+ ,函数在(0,1]递减
,函数在(0,1]递减 (当且仅当t=1即θ=
(当且仅当t=1即θ=| π |
| 4 |
 时,
时,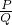 的最小值为
的最小值为 .
. ,AC=atanθ,x,即可求出三角形ABC的面积P,正方形的面积Q.
,AC=atanθ,x,即可求出三角形ABC的面积P,正方形的面积Q.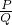 的表达式,利用函数的单调性,求出比值的最小值.
的表达式,利用函数的单调性,求出比值的最小值.

科目:高中数学 来源: 题型:
 如图所示,在Rt△ABC内有一内接正方形,它的一条边在斜边BC上,设AB=a,∠ABC=θ
如图所示,在Rt△ABC内有一内接正方形,它的一条边在斜边BC上,设AB=a,∠ABC=θ| f(θ) | g(θ) |
查看答案和解析>>
科目:高中数学 来源: 题型:
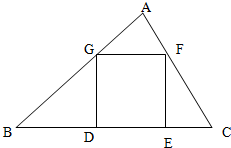 在Rt△ABC内有一内接正方形,它的一条边在斜边BC上,如图所示.
在Rt△ABC内有一内接正方形,它的一条边在斜边BC上,如图所示.| P | Q |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| f(θ) |
| g(θ) |

查看答案和解析>>
科目:高中数学 来源:2012-2013学年广西贺州高级中学高一(下)期末数学试卷(理科)(解析版) 题型:解答题
 的最小值.
的最小值.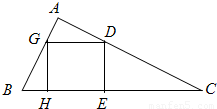
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省新余一中高一(下)第一次段考数学试卷(4月份)(解析版) 题型:解答题
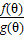 的最小值.
的最小值.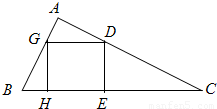
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com