
| A.对立事件 |
| B.不可能事件 |
| C.互斥但不对立事件 |
| D.以上答案均不对 |
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
 两条巷道通往作业区(如下图),
两条巷道通往作业区(如下图), 巷道有
巷道有 三个易堵塞点,各点被堵塞的概率都是
三个易堵塞点,各点被堵塞的概率都是 ;
; 巷道有
巷道有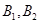 两个易堵塞点,被堵塞的概率分别为
两个易堵塞点,被堵塞的概率分别为 .
.
 巷道中,三个易堵塞点最多有一个被堵塞的概率;
巷道中,三个易堵塞点最多有一个被堵塞的概率; 巷道中堵塞点个数为
巷道中堵塞点个数为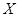 ,求
,求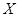 的分布列及数学期望
的分布列及数学期望 ,并按照"平均堵塞点少的巷道是较好的抢险路线"的标准,请你帮助救援队选择一条抢险路线,并说明理由.
,并按照"平均堵塞点少的巷道是较好的抢险路线"的标准,请你帮助救援队选择一条抢险路线,并说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,乙能攻克的概率为
,乙能攻克的概率为 ,丙能攻克的概率为
,丙能攻克的概率为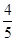 .
. 万元。奖励规则如下:若只有1人攻克,则此人获得全部奖金
万元。奖励规则如下:若只有1人攻克,则此人获得全部奖金 万元;若只有2人攻克,则奖金奖给此二人,每人各得
万元;若只有2人攻克,则奖金奖给此二人,每人各得 万元;若三人均攻克,则奖金奖给此三人,每人各得
万元;若三人均攻克,则奖金奖给此三人,每人各得 万元。设甲得到的奖金数为X,求X的分布列和数学期望。(本题满分12分)
万元。设甲得到的奖金数为X,求X的分布列和数学期望。(本题满分12分)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.是互斥事件,不是对立事件 | B.是对立事件,不是互斥事件 |
| C.既是互斥事件,也是对立事件 | D.既不是互斥事件不是对立事件 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.0.35 | B.0.42 | C.0.85 | D.0.15 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.0.62 | B.0.38 | C.0.02 | D.0.68 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
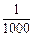 ,意味着买
,意味着买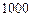 张彩票一定能中奖;
张彩票一定能中奖;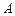 为“恰有1个白球”,记事件
为“恰有1个白球”,记事件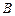 为“恰有2个白球”,则
为“恰有2个白球”,则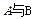 为互斥而不对立的两个事件。
为互斥而不对立的两个事件。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com